En Agriculture de Précision, la délimitation de zones intra-parcellaires est devenue une étape assez classique dans les chaines de traitement des services proposés sur le marché (Figure 1). La création de zones permet surtout de répondre à demandes opérationnelles. Ces zones permettent déjà de simplifier la lecture d’une carte d’agriculture de précision parce que cela permet de prendre un peu de recul sur les données sous-jascentes et d’avoir une vision plus globale des grandes tendances à l’œuvre dans une parcelle. Il est également plus simple de recouper ces zones avec d’autres sources d’information spatialisées pour en tirer des conclusions. L’agronome a alors face à lui une carte simplifiée sur laquelle il peut décider d’une action à mettre en place sur chaque grande unité de gestion (les zones). Toujours d’un point de vue opérationnel, ces cartes zonées peuvent être également envoyées sur des machines agricoles (notamment parce que ce format est assez léger et peut-être lu par les machines) pour des applications de modulation intra-parcellaire en tout genre (semis, fertilisation, pulvérisation…)
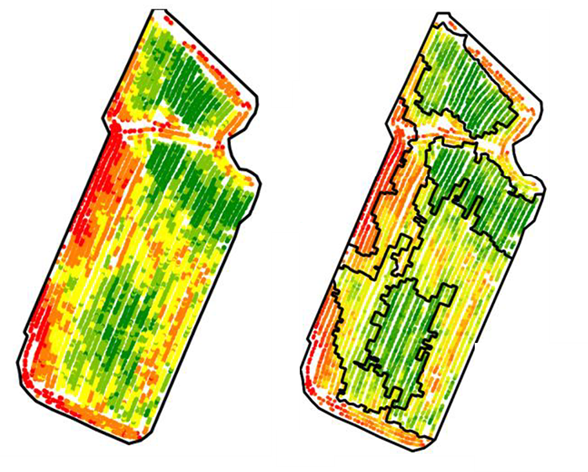
Figure 1. Carte de rendement (gauche) et zonage associé (droite)
La délimitation de zones intra-parcellaires n’est pas quelque chose de tout simple. Cela pourrait paraitre surprenant de prime abord parce que tout le monde est capable, en regardant une carte colorisée, de distinguer des grandes unités ou des grandes zones sur une parcelle (Figure 1). Mais en réalité, sur quoi se base-t-on ? Sur des différences de couleur ? Sur des différences de formes ? Sur des gradients que l’on a l’impression d’entrevoir ? Est-ce qu’au final, nos yeux ne pourraient pas être un peu trompés par les couleurs affichées sur la carte, et donc pas la méthode de colorisation appliquée (c’est d’ailleurs un projet qu’il serait intéressant d’étudier, avis aux amateurs) ? La variabilité que l’on observe au sein de la parcelle est-elle significative ou en d’autres termes, les zones que je vois et que je peux dessiner à l’œil nu ont-elles du sens d’un point de vue agronomique, et est ce qu’elles peuvent être travaillées d’un point de vue opérationnel ? Qu’est ce qu’une zone après tout, si ce n’est une sorte de forme inerte dans la parcelle ? En quoi une zone doit être différente de ces voisines ? Quand on commence à pousser un peu loin, on pourrait même rentrer dans des débats philosophiques !
Zonage classique
Passons maintenant à la technique parce qu’informatiquement, la construction de ces zones intra-parcellaire est légèrement plus compliquée que visuellement. J’en avais déjà parlé brièvement dans un précédent post de blog mais on peut distinguer deux grandes typologies de méthodes pour réaliser ces cartes de zonage : les approches par classification, et les approches par segmentation.
Les méthodes de classification (principalement intervalles égaux, quantiles, jenks, ou k-moyennes ; il y en a d’autres) sont puissantes pour séparer des valeurs en différentes classes. Ces approches sont souvent utilisées parce qu’elles sont relativement faciles à mettre en œuvre et à paramétrer (avec un nombre de classes à renseigner par exemple). Malgré tout, si vous êtes amenés à en utiliser, force est de constater que ces approches génèrent souvent des zones fragmentées – une sorte d’effet un peu poivre et sel – parce que ces méthodes ne tiennent pas compte des relations spatiales entre les données (c’est un peu ce qu’on voit sur la carte gauche de la figure 1, les données sont colorisées pour qu’on y voit quelque chose donc elles ont été classifiées). La classification est en effet réalisée sur les valeurs attributaires et pas sur la position des données dans l’espace. Il y a plusieurs façons de se sortir de cet embarras. La plus communément choisie est de lisser les données (avant ou après classification) pour justement limiter cet effet poivre et sel. Ce lissage peut se faire par interpolation si les données sont ponctuelles (des données de sol ou de rendement par exemple) ou par le passage de différents filtres (filtres moyens, médians ou autres) si les données sont sous la forme de rasters. Ce post-traitement est intéressant parce qu’il permet d’arriver à une carte plus propre d’un point de vue opérationnel mais ça n’est pas toujours évident d’arriver automatiquement à une carte convenable tout simplement parce que le niveau de filtre va aussi dépendre des données d’entrée. On se retrouve donc souvent avec des cartes parfois trop filtrées, parfois pas assez, si les paramètres de filtres sont les mêmes. Une deuxième façon de s’en sortir est de réaliser une classification en prenant en compte non seulement la valeur attributaire des données mais aussi la position des données dans l’espace. L’inconvénient majeur ici est qu’il n’est pas évident de choisir le poids à accorder à chacune de ces variables (position X, position Y, attribut). De manière générale, on arrive à s’en sortir avec les méthodes de classification, mais ce ne sont quand même pas des méthodes faites à la base pour du zonage de données spatiales. Et rajoutons à cela que quelles que soient les données, il sera toujours possible de les classer, même s’il y a très peu de variabilité. Autrement dit, quand on cherche de la variabilité, on la trouve toujours…
Les approches de segmentation sont quant à elles plus adaptées au zonage de données spatiales. Ces méthodes sont souvent issues du domaine du traitement d’images où l’on cherche à délimiter des formes relativement bien définies. Vous avez peut-être déjà vu la belle Lena sur une des images de références en traitement d’images, l’objectif étant de discriminer chaque élément de l’image (Figure 2). Pas évident entre le chapeau, les plumes, les cheveux ou encore le visage.

Figure 2. Lena, une référence en traitement d’images
Le problème, vous l’aurez peut-être compris, c’est qu’une zone en agriculture de précision, ce n’est pas quelque chose de très bien défini… mais au moins on peut s’inspirer de ce qui est proposé dans la littérature de traitement d’images pour faire du zonage. On y retrouve énormément d’approches différentes dont :
- des méthodes par croissance de régions (on place des sortes de graines ou de points de départ un peu partout sur une parcelle et on fait grossir ces structures de proche en proche jusqu’à obtenir des zones – un peu comme une tache d’huile qui s’épandrait),
- des méthodes plutôt orientées découpage d’images du genre « quadtree » (où à l’inverse, on découpe la parcelle en plein de petits pavés de tailles différentes jusqu’à arriver à des zones), ou encore
- des méthodes basées sur la recherche de contours (dans ce cas-là, on cherche les frontières entre les zones, et les zones sont donc trouvées indirectement).
Il arrive régulièrement que ces approches génèrent pas mal de zones, et il est souvent nécessaire de fusionner en partie les zones construites pour arriver à un résultat plus opérationnel avec moins de zones (Figure 3)
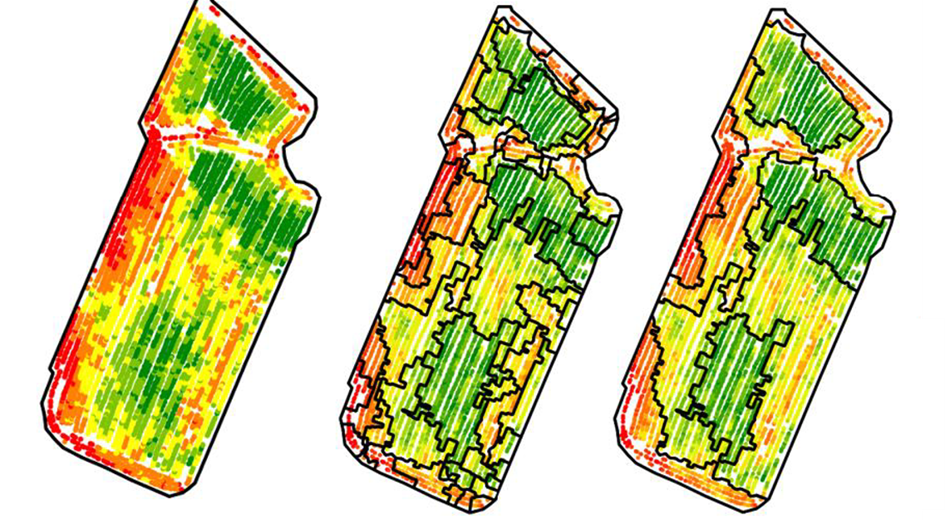
Figure 3. Exemple d’approche de zonage. Zonage après croissance de régions (au milieu) puis fusion de zones (à droite) Contrairement aux approches de classification, les approches de segmentation tendent à produire des unités spatiales plus faciles à gérer et moins fragmentées (moins d’effet poivre et sel) parce que la localisation spatiale de chaque observation ainsi que les relations spatiales de voisinage entre chaque observation sont considérées (Figure 3). Ce sont néanmoins des approches un peu plus complexes à mettre en œuvre et à paramétrer que les approches de classification. Pour ceux que ça intéresse, je vous invite à aller regarder un de mes articles de thèse et les références associées
Quelques éléments complémentaires ! Le zonage peut être appliqué sur tout type de données, que ce soient des données ponctuelles ou des données rastérisées. Les approches sont sensiblement différentes puisque lorsque l’on travaille avec des données raster, on peut appliquer directement des approches issues du traitement d’images. Avec des données ponctuelles, il faut soit passer par une étape préalable d’interpolation (pour obtenir un raster), soit développer une approche spécifique pour des données ponctuelles (c’est ce que nous avons proposé dans ma thèse). A côté de ça, j’ai présenté jusque-là du zonage univarié, c’est-à-dire que l’on cherche à construire des zones sur un attribut donné (par exemple une carte de rendement). Mais rien n’empêche de mettre en place des actions de zonage multivarié, en considérant en même temps plusieurs attributs (un zonage basé à la fois sur une carte de sol et de rendement) ou alors un même attribut dans le temps (un zonage basé sur un historique de cartes de rendement) [Figure 4]
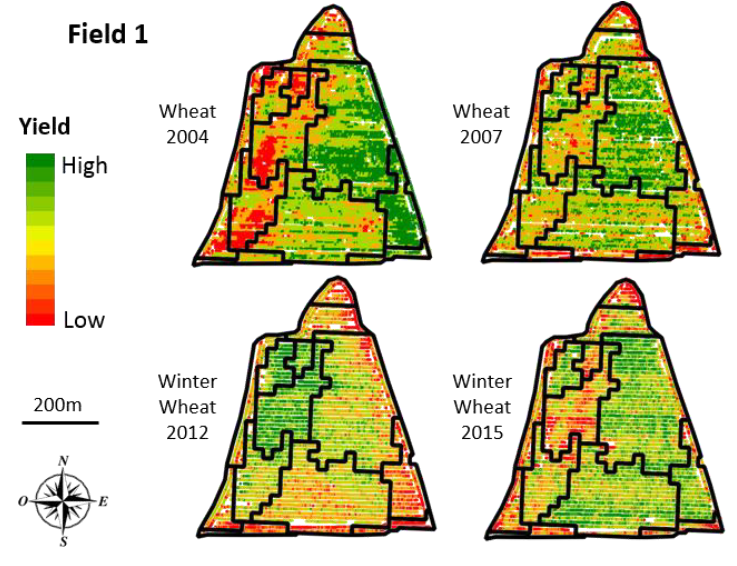
Figure 4. Zonage multi-temporel de données de rendement
J’aimerais insister également sur la différence entre une classe et une zone (Figure 5). Vous pourrez me dire que ce sont des considérations un peu trop théoriques mais je considère quand même que les mots ont leur importance, et ça explique notamment ce qu’on observe avec des méthodes de classification ou de segmentation. Une zone, c’est une entité contiguë et fermée. Une classe, c’est un label, c’est la valeur attributaire d’une zone. On peut donc très bien avoir plusieurs zones avec la même classe. C’est important à considérer parce que c’est ce pour quoi les approches de classification tendent à générer un effet poivre et sel. Les approches de classification ne créent pas directement des zones, elles le font indirectement en réalité. (Figure 5). On devrait donc dire que ceux qui utilisent des méthodes de classification construisent des classes intra-parcellaires, que des zones intra-parcellaires.
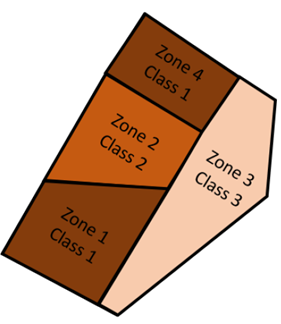
Figure 5. La différence entre une zone et une classe
Après ces quelques notions générales, j’avais envie d’introduire des concepts pour aller un peu plus loin dans le zonage. Ce ne sont pas des approches complètement opérationnelles, mais ce pourraient être des idées à creuser. Nous allons discuter ici de logique floue et de programmation par contraintes, et les appliquer au zonage !
Zonage flou
Cette section est un résumé vulgarisé d’un article scientifique que nous avions proposé à la conférence européenne d’agriculture de précision en 2019
Lorsque l’on délimite des zones intra-parcellaires en agriculture de précision, on aimerait que ces zones soient les plus différentes possibles de leurs voisines, de manière à ce que chaque zone soit la place d’une action différentiée. Mais en agriculture, il est quand même assez rare d’observer des découpes très nettes dans les parcelles. Tout dépend en réalité des paramètres agronomiques et/ou pédologiques auxquels on s’attarde. On peut bien évidemment avoir des veines de sol, des unités de sol, ou encore des conditions de pédogènèse extrêmement différentes au sein d’une parcelle. Mais lorsque l’on regarde des attributs de végétation (vigueur, biomasse, rendement…), ou de topographie (altitude, pente…), on aura quand même souvent affaire à des gradients, à des grandes tendances pas si nettes que ça. Et pour vous en convaincre, vous pouvez réaliser des tests rapidement avec des collègues. Prenez une cartographie à haute résolution (une carte de végétation ou de rendement par exemple), et demandez à plusieurs de vos collègues de délimiter 4-5 zones dedans. Vous vous rendrez compte que personne ne fera exactement les mêmes. Bien évidemment, le centre ou le cœur des zones sera bien identifié (peut-être moins si vos collègues sont daltoniens, mais c’est un autre débat), mais le contour des zones sera plus ou moins différent. En agriculture de précision, les limites entre les zones sont donc plutôt assez floues. Les observations proches des limites de chaque zone pourraient donc appartenir à plus d’une zone, tout dépend ce dont on veut faire de ces zones. En fonction d’un opérateur ou d’une opération culturale particulière, l’objectif au sein de la parcelle ne sera pas le même et il n’y a donc pas de raison pour que ces zones soient identiques. Prenons l’exemple de la parcelle ci-dessous, pour laquelle les observations de rendement sont affichées (Figure 6). Des zones ont été pré-délimitées avec un algorithme de croissance de régions (celui de l’article de zonage de ma thèse cité plus haut).
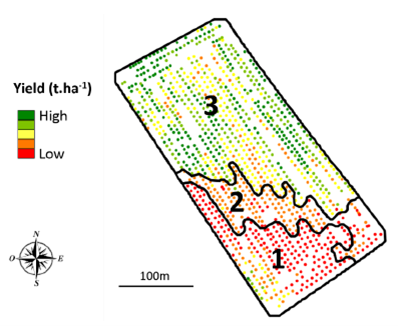
Figure 6. Zonage d’une carte de rendement.
L’algorithme utilisé a conduit à la création de 3 zones à l’intérieur de la parcelle. On se rend compte que le rendement est relativement fort sur le nord de la parcelle, moyen sur la diagonale est/ouest et assez faible au sud de la parcelle. La zone 2 semble même plutôt être une zone de transition entre la zone 1 et la zone 3, plus qu’une zone vraiment à part entière. On voit également que dans la zone 3, les observations au centre de la parcelle et proches de la zone 2 sont affichées en jaune et on peut se demander pourquoi ces observations ne pourraient pas également appartenir à la zone 2. On observe aussi une zone de rendement qui a l’air moyennement forte au sud-ouest de la zone 1 mais cette petite entité n’a pas été délimité par l’algorithme de croissance de régions utilisé (cet endroit a donc surement été considéré comme trop petit par l’algorithme pour être délimité comme une zone, ne le considérons donc pas).
Pour visualiser cette notion d’appartenance de chaque observation à une zone, nous avons sélectionné aléatoirement une observation au sein de chaque zone, et nous avons relancé l’algorithme de croissance de régions (croissance de proche en proche un peu comme une tache d’huile). Avec 3 observations au départ (1 observation par zone), le rendu final était forcément constitué de 3 zones. Et nous avons relancé cette approche 100 fois. Nous avons donc obtenu 100 zonages différents, et nous avons compté le nombre de fois où chaque observation appartenait à la même zone qu’une des 3 observations initiales. La carte des degrés appartenances (de 0 à 1 – ce sont des pourcentages) de chaque observation à une zone est présentée dans la figure 7.
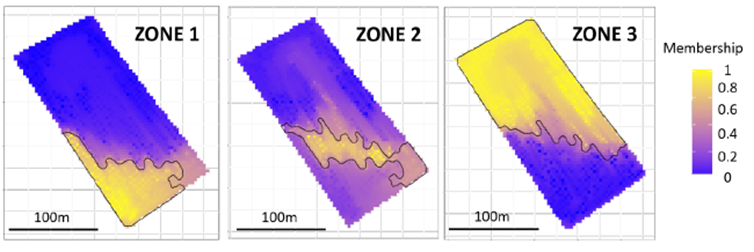
Figure 7. Degré d’appartenance de chaque observation à une zone
Au sein de cette carte, nous voyons clairement apparaitre le cœur de chaque zone. Ce sont les endroits très marqués en jaune, c’est-à-dire les endroits pour lesquels les observations sont toujours dans la même zone quoi qu’il arrive. Par exemple, pour la zone 1, ce sont les observations au sud-ouest de la parcelle. Pour la zone 3, ce sont les observations au nord. A l’inverse, les endroits très marqués en bleus sont ceux pour lesquels les observations n’appartiennent jamais à la zone. Les observations au sud de la parcelle n’appartiennent par exemple jamais à la zone 3. Et puis il y a tout l’entre deux ! Par exemple, on se rend compte à quel point le cœur de la zone 2 est petit mais l’étendue peut être grande (d’un point de vue terminologique, on différencie le « cœur » ou noyau de la zone et son « support » ou son étendue). Pour cette zone 2, il y a pas mal de cas où des observations de la zone 1 ou 3 peuvent aussi appartenir à la zone 2. Les supports des zones 1 et 3 sont quant à eux plus petits. En d’autres termes, les zones 1 et 3 sont bien définies et relativement claires, contrairement à la zone 2 (on s’en doutait néanmoins parce que cette zone ressemblait pas mal à une zone de transition entre les zones 1 et 3).
Que faire de cette carte de degrés d’appartenance ? Et bien, pourquoi ne pas considérer des cas d’étude spécifiques pour voir à quel point certains zonages pourraient être plus adaptés que d’autres. Prenons le cas n°1 où l’on va considérer que l’agriculteur est soumis à de fortes contraintes environnementales et qu’il ne peut accepter aucun risque de surdosage. Dans ce cas n°1, les zones doivent être limitées à leur noyau. Dans le cas n°2, l’agriculteur utilise un engrais à faible coût dont les risques pour l’environnement ou les répercussions sur le rendement sont limitées. Les zones peuvent donc être étendues à leur support. En considérant ces deux cas, et en fixant des seuils de degré d’appartenance, on peut construire des cartes d’application pour chaque zone (Figure 8). Que ce soient pour la zone 1 ou la zone 3, on se rend compte à quel point le contour de ces zones peut changer en fonction du cas d’usage considéré. Prenons l’exemple de la zone 3 (sur la ligne du bas de la figure 8). Un degré d’appartenance supérieure à 0.3 est considéré comme représentant le cas d’étude n°2 parce qu’une observation appartient à la zone 3 si, dans au moins 30% des cas, l’observation est associée à la zone 3 (le support ou l’étendue de la zone est donc grand). A l’inverse, un degré d’appartenance supérieure à 0.7 est considéré comme représentant le cas d’étude n°1 parce qu’il faut au moins 70% de cas où l’observation est associée à la zone 3 pour qu’on considère qu’elle y appartienne (le support de la zone est donc plus petit ; on se rapproche de son cœur) Le même raisonnement peut être appliqué pour la zone 1.
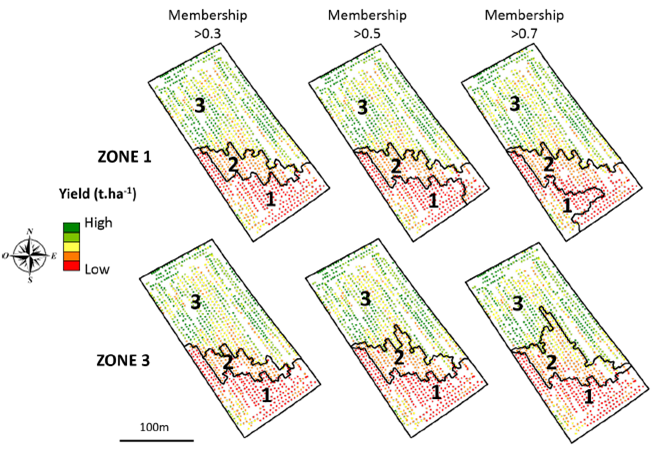
Figure 8. Adaptation du zonage aux cas d’usage.
Ces résultats dépendent bien évidemment du zonage initial (Figure 6), ou encore des seuils d’appartenance fixés, mais ce travail permet de mettre en évidence la notion de floue associée au zonage intra-parcellaire, et propose une façon de la prendre en compte. Si ça vous donne des idées ou si ça vous inspire, n’hésitez pas à partager des commentaires !
Zonage sous contraintes
Cette section est un résumé vulgarisé d’un article scientifique que nous avons proposé à la conférence européenne d’agriculture de précision en 2021.
Lorsque l’on délimite des zones intra-parcellaires en agriculture de précision, on se doit de définir ce que l’on cherche à obtenir. Globalement, on cherche les zones qui représentent au mieux la variabilité de la parcelle, c’est-à-dire des zones qui soient le plus homogènes possibles et le plus différentes de leurs voisines possibles. C’est déjà bien mais une fois qu’on a dit ça, on n’est pas non plus super avancé :
- Sur quoi juge-t-on l’homogénéité d’une zone ? Sur sa variance ? Sur une somme d’écarts entre chaque observation et la moyenne de la zone ?
- Sur quoi juge-t-on la différence entre deux zones voisines ? Sur la différence de moyenne entre les deux zones ? Sur la différence maximale entre deux observations, chacune appartenant à une zone ? Sur l’écart entre les zones, observation par observation ?
- Et puis, sur les zones en elles-mêmes, est-ce que l’on veut un nombre de zones spécifique sur la carte finale ? Est-ce que l’on veut des zones qui ont une taille minimale ? Est-ce que l’on veut des zones avec une forme assez géométrique pour pouvoir les travailler de façon opérationnelle ?
Bref, ça fait beaucoup de questions et on peut commencer à entrevoir les limites des approches de classification ou de zonage. Déjà parce que l’on se rend compte qu’au vu du nombre de questions qu’on peut se poser ici, il y a peu de chances que le paramétrage relativement simple de ces approches parvienne à nous satisfaire. Et puis parce que dans bien des cas, on se retrouve à rajouter dans notre chaine de traitement plusieurs étapes successives (du post-traitement) pour répondre à toutes ces demandes (par exemple, on supprime les zones de trop petite taille). En agissant de la sorte, on a un peu l’impression de ne pas prendre le problème à sa racine, mais d’agir comme un pompier en rajoutant des étapes dès qu’il y a un problème. Et ce n’est pas la seule limite de ces approches. Pour ceux qui seront intéressés à l’approche de zonage par croissance puis fusion de zones que j’ai proposée dans ma thèse (Figure 3), vous vous rendrez compte que la fusion de zones suit un processus itératif. Les zones sont fusionnées au fur et à mesure en maximisant un critère opérationnel (qui prend en compte l’écart entre chaque observation et la zone à laquelle elle appartient et fait en sorte d’aboutir à des zones plutôt géométriques ; je vous invite à vous y pencher un peu plus si ça vous intéresse). La principale limite étant qu’une fois qu’une zone est fusionnée, on ne peut pas revenir en arrière. On aboutit donc potentiellement à la fin à une carte zonée qui est plutôt un optimum local qu’un optimum global. C’est-à-dire qu’à chaque fois qu’une zone est fusionnée, la fusion suivante est celle qui maximise le nouveau critère opérationnel ; on voit ici que ce n’est pas une optimisation globale du zonage, mais une optimisation à chaque itération, ce qui n’est pas exactement la même chose. Rien ne nous dit en effet qu’une meilleure carte zonée n’aurait pas pu être obtenue en partant d’une fusion un peu moins bonne au départ. C’est la limite des approches incrémentales. Et c’est sans compter le fait que la fusion des zones ne prend en compte que ce critère opérationnel. Si on voulait un nombre de zones spécifiques, il faudrait faire une fusion toujours en maximisant ce critère opérationnel mais en arrêtant la fusion quand on obtient le nombre de zones voulu.
Une façon de se sortir de ce fatras est de s’intéresser à la programmation par contraintes. Comme son nom l’indique, on met en place des contraintes à notre algorithme et on le force à nous trouver une solution optimale qui répond aux contraintes fixées. Pour se faire, nous avons besoin de définir une fonction d’optimisation (c’est-à-dire ce que l’algorithme va essayer d’optimiser) et un ensemble de contraintes dont l’algorithme devra tenir compte. Appliquons donc ça au zonage de données ! Nous allons repartir d’un zonage obtenu à partir d’une croissance de régions (Figure 9) et nous allons tenter de fusionner les zones obtenues (qui sont trop nombreuses) à l’aide d’une méthode de programmation par contraintes.
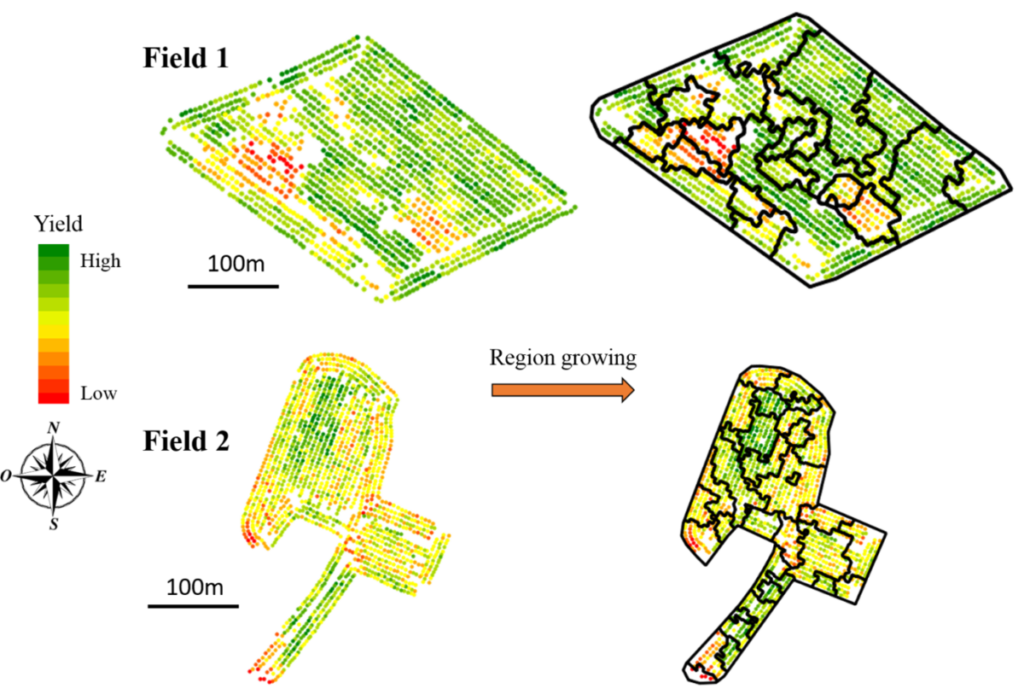
Figure 9. Cartes de rendement ponctuelles et zonages associés (issus d’un algorithme de croissance de régions).
Je me permets ici de présenter la méthode sous la forme de notations et d’équations parce que je pense que c’est une forme assez lisible. Si vous n’êtes pas à l’aise avec les équations, le texte devrait vous suffire à bien comprendre les contraintes et la fonction d’optimisation mise en place.
L’objectif principal de l’algorithme de fusion sous contraintes est de générer un ensemble de k zones finales Z_i (i \in [1:k]; k \leq N) à l’intérieur de la parcelle (N est le nombre de zones initiales).
Commençons par quelques notations:
- Chaque zone initiale S_j issue de l’algorithme de croissance de régions est constituée de plusieurs observations spatiales (faites bien la différence entre les zones initiales S_j et les zones finales Z_i). Chacune des observations p dans S_j a une valeur de rendement appelée A(p)
- La contiguïté entre les unités spatiales S_j est décrite par le graphe G = (V,E)
- Pour chaque unité spatiale S_j
- area(S_j) est l’aire de S_j
- card(S_j) est le nombre d’observations dans S_j
- \mu(S_j) est la valeur moyenne du rendement des points appartenant à S_j
\mu(S_j)=\frac{1}{card(S_j}\sum_{p \in S_j} A(p)
- Et
- SSE(S_j) est la somme des erreurs au carré au sein de S_j
SSE(S_j)=\sum_{p \in S_j} (A(p)-\mu(S_j))^2
Les contraintes de l’algorithme : Maintenant que les notations sont clarifiées, passons aux contraintes ! Pour avoir des zones cohérentes avec des problématiques opérationnelles sur le terrain, on va considérer ici que les zones finales Z_i doivent être suffisamment grandes (seuil \alpha et que deux zones voisines/adjacentes doivent avoir des valeurs de rendement sensiblement différentes pour que ces zones puissent recevoir des applications différentes (seuil \beta). Les deux paramètres \alpha et \beta sont considérés comme des seuils experts et apparaissent dans les contraintes n°3 et n°5.
- Contrainte n°1 : Les zones finales Z_i ne peuvent pas être vides
\forall i \in \{1:k\}, Z_i \ne \emptyset
- Contrainte n°2 : Les zones finales Z_i sont disjointes (chacune est bien séparée des autres) et chaque zone initiale S_j appartient à une des zones finales Z_i (c’est plutôt logique parce que les zones Z_i sont le résultat de la fusion des zones initiales S_j
\{Z_i\}_{(i \in 1...k)} est une partition de \{1...N\}
- Contrainte n°3 : La surface des zones finales Z_i doit être supérieur au seuil \alpha
\forall i \in \{1:k\}, \sum_{S_j \in Z_i} area(S_j) \geq \alpha
- Contrainte n°4 : Toutes les zones initiales S_j qui appartiennent à la même zone finale Z_i doivent être connectées les unes aux autres. Le graphe G induit par chaque zone Z_i est donc lui aussi connecté (cette contrainte ressemble un peu à la contrainte n°2 pour s’assurer qu’une zone finale est constituée de zones initiales voisines, sinon ça n’aurait pas de sens).
\forall i \in \{1:k\}, G[Z_i] est connecté
- Contrainte n°5 : La différence de rendement entre deux zones voisines doit être supérieur au seuil \beta
\forall i1,i2 \in \{1:k\}, i1 \ne i2, Z_1 ADJ Z_2 \Rightarrow \vert \mu({Z_i}_1) - \mu({Z_i}_2) \vert \geq \beta
Avec ADJ la relation d’adjacence :
Z_1 ADJ Z_2 \Leftrightarrow \exists {S_j}_1 \in Z_1, \exists {S_j}_2 \in Z_2 tel que (j_1,j_2) \in E
La fonction d’optimisation de l’algorithme : L’approche de programmation par contraintes vise à fusionner de manière optimale les zones initiales afin de minimiser la fonction \f qui est la somme des carrés des écarts entre le rendement de chaque observation et le rendement moyen de la zone à laquelle appartient l’observation :
f = \sum_{i \in 1...k} SSE(S_j) = \sum_{i \in 1...k} \sum_{p \in U_(S_j \in Z_i)} (A(p) - \mu(Z_i))^2
Pour les tests que nous avons réalisés, nous avons choisi de fixer les seuils \alpha et \beta respectivement à 0.5 ha (surface minimale de zones) et 1 tonne par ha (différence minimale de rendement entre zones voisines). Pour faire tourner des algorithmes de programmation par contraintes, il faut en général utiliser un solveur qui contient déjà des modules d’optimisation et qui est capable de prendre en compte des contraintes. On ne peut pas faire tourner très simplement un algorithme de programmation par contraintes sur des langages comme R ou Python. Dans notre cas, nous avons utilisé un solveur du nom de « Choco », qui semblait plutôt adapté à notre problématique. Les résultats d’optimisation sous contraintes sont présentés dans les figures 10 et 11. Il est intéressant de noter que l’algorithme n’est pas toujours capable de trouver de solutions aux contraintes qu’on lui a fixées. C’est déjà pas mal ! Ca veut dire par exemple que pour la parcelle 2, on ne peut pas trouver de zonage à plus de 4 zones qui respectent nos contraintes de surface minimale de 0.5 ha et de différence minimale de rendement de 1 tonne par ha. Lorsque l’on a ces résultats à disposition, il y a plusieurs façons de les considérer. Soit on veut travailler avec un nombre de zones particulier et on sélectionne donc le zonage correspondant. Soit on cherche parmi les résultats celui avec la valeur de la fonction f la plus faible (puisqu’on a cherché à minimiser f pour chaque nombre de zones dans la parcelle), indépendamment du nombre de zones. Dans le cas de la parcelle 1 par exemple, la fonction f atteint un minimum pour 5 zones avant de remonter assez fortement pour 6 zones. Nous n’avons pas comparé ici ces résultats à ceux d’une méthode de zonage plus classique (mais on sait déjà que la méthode classique aurait donné des résultats quel que soit le nombre de zones demandé).

Figure 10. Optimisation sous contraintes (Parcelle 1) entre 3 et 7 zones.

Figure 11. Optimisation sous contraintes (Parcelle 2) entre 3 et 7 zones.
Dans ce petit cas d’étude, nous avons seulement fixé des contraintes sur la taille des zones et la différence attributaire entre deux zones voisines (les contraintes n°1, 2 et 4 sont plutôt associées au problème du zonage en général et il faudra donc toujours les garder). On aurait pu en considérer d’autres, par exemple sur la forme des zones, ou sur la variabilité maximale au sein de chacune des zones. Tout est possible. Il faut néanmoins s’assurer que les contraintes ont un sens d’un point de vue agronomique et opérationnel. Notez également que la programmation par contraintes est intéressante, mais qu’elle prend nécessairement plus de temps que des approches de zonage plus classiques. Le solveur aide à accélérer et améliorer la recherche de solutions optimales mais cela prend du temps puisqu’il faut prendre en compte des contraintes. Et plus il y a de contraintes, plus le temps de recherche peut être long.
Le zonage intra-parcellaire soulève un nombre de questions importantes quand on commence à s’y pencher un peu. Entre des limites de zones assez floues, des contraintes opérationnelles à intégrer, ou encore la possibilité de travailler en uni ou multivarié, le sujet est loin d’être traité entièrement. Gardez néanmoins en tête que plusieurs de ces travaux restent exploratoires (notamment les sections sur le zonage flou et le zonage sous contraintes). Leur implémentation et industrialisation reste tout à fait possible. Encore faut-il qu’elle soit pertinente pour la profession, qu’elle apporte vraiment une plus-value par rapport aux approches classiques, et qu’elle ne rende pas l’analyse de zones intra-parcellaires encore plus complexe qu’elle ne l’est actuellement.
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

