Simulation de données spatiales avec une structure spatiale connue

La simulation de jeux de données avec une structure spatiale connue est une stratégie intéressante lorsque l’on cherche à évaluer, de manière objective, la pertinence d’une méthode de traitement de données. L’avantage majeur des simulations est de pouvoir contrôler la distribution des données au sein de la parcelle et donc de contrôler le contexte autour duquel la méthode de traitement de données est appliquée.

Par exemple, on pourrait vouloir évaluer la capacité d’une méthode de filtrage de données aberrantes à détecter des observations dans des jeux de données de rendement.

Le package gstat de R fournit des fonctions puissantes et efficaces pour simuler des jeux de données spatiales. Pour rappel, en agronomie, les données spatialisées (rendement, conductivité du sol, topographie…) sont souvent auto-corrélées, c’est à dire que des observations proches dans l’espace partagent souvent des caractéristiques plus proches que des observations plus éloignées. Le package gstat peut être utilisé pour simuler des champs aléatoires gaussiens (le terme généralement utilisé par les spécialistes du domaine) à partir d’un algorithme de simulation séquentielle (Bivand et al., 2013) ¹. Cette approche demande de définir un modèle pour le semi-variogramme qui sera utilisé pour créer les champs gaussiens aléatoires. L’algorithme de simulation séquentielle utilise un modèle de variogramme et les valeurs simulées en amont pour calculer la distribution conditionnelle des futures observations à prédire. Une nouvelle observations est sélectionnée dans cette distribution conditionnelle et ajoutée au jeu de données. Ces étapes sont répétées jusqu’à ce que toutes les observations reçoivent une valeur (Bivand et al., 2013). A noter cet autre post qui s’intéresse de près à la simulation de champs gaussiens aléatoires sur R (et qui a bien servi à aggrémenter ce post).

## Charger le package gstat
library(gstat)
## Créer une parcelle carrée de côté 100. Cette parcelle peut être vue comme une grille de pixels régulièrement répartis dans l'espace.
Field = expand.grid(1:100, 1:100)
## Donner un nom aux coordonnées spatiales dans la parcelle
names(Field)=c('x','y')
 
## Définir la structure spatiale du rendement dans la parcelle
   ## Choix des paramètres du semi-variogramme
      Psill=15  ## Partial sill (Pallier partiel) = Amplitude de variation
      Range=30  ## Portée pratique = Distance maximale d'auto-corrélation
      Nugget=3  ## Effet pépite = Variations à petite échelle (courtes distances)
   ## Paramétrage du modèle de semi-variogramme
      Beta=7   ## moyenne de rendement (tonnes/ha) sur la parcelle
      RDT_modelling=gstat(formula=z~1, ## On assume qu'il y a une tendance constante sur la parcelle
                           locations=~x+y,
                           dummy=T,    ## Valeur binaire qui doit être réglée sur True (Vrai) pour la simulation non conditionnelle
                           beta=Beta,  ## Réglage de la moyenne de la variable d'intérêt sur la parcelle
                           model=vgm(psill=Psill, ## Pallier partiel
                                     range=Range , ## Portée pratique
                                     nugget=Nugget, ## Effet pépite
                                     model='Sph'), ## Modèle sphérique pour le semi-variogramme
                           nmax=40) ## Nombre de voisins à prendre en compte pour les prédictions
 
## Simuler la structure spatiale de NDVI au sein de la parcelle
RDT_gaussian_field=predict(RDT_modelling, newdata=Field, nsim=1) ## nsim : Nombre de simulations

La variable RDT_gaussian_field est un dataframe qui contient, pour chaque observation au sein de la parcelle (pour chaque pixel), ses coordonnées spatiales et la valeur de rendement associée. De manière à afficher la structure spatiale simulée, le package ggplot2 peut être utilisé comme suit :

## Charger la librarie ggplot2
library(ggplot2)
 
## Afficher la parcelle
ggplot()+  ## Initialiser la couche ggplot
geom_point(data=RDT_gaussian_field,aes(x=x,y=y,col=sim1))+ ## Afficher les observations sous forme de points avec un gradient de couleur de rendement
scale_colour_gradient(low="red",high="green")   ## Régler les couleurs du gradient

Une simple itération de la simulation a conduit à la parcelle suivante (Fig. 1):

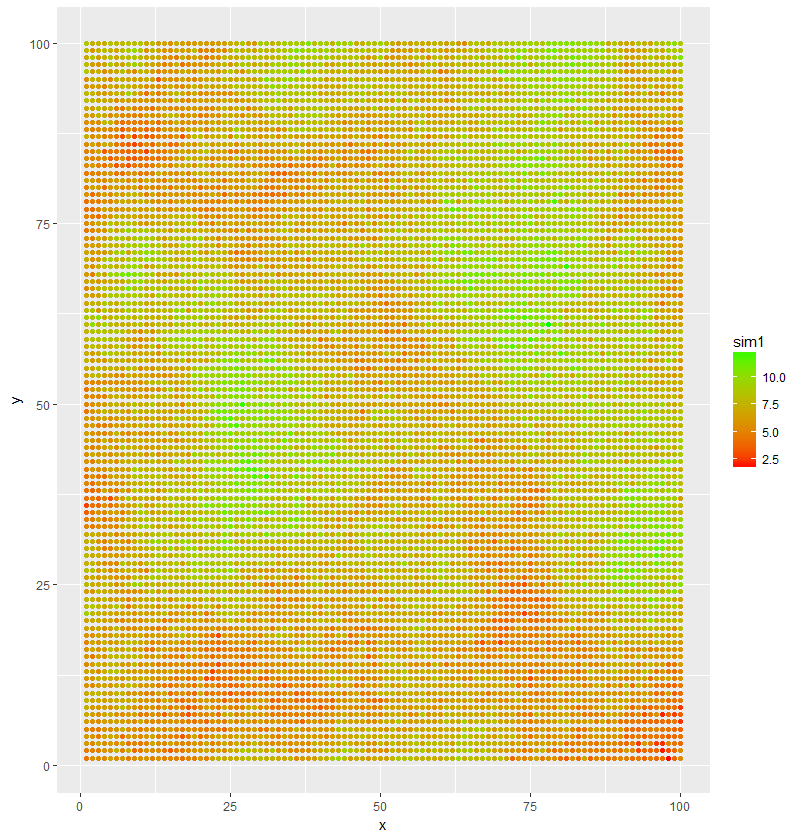
Figure 1. Cartographie de rendement simulée avec les paramètres précédemment établis

Il faut bien comprendre que la simulation a pour objectif de récréer une structure spatiale avec les paramètres du variogramme qui ont été choisis. Néanmoins, il peut arriver que la structure spatiale dévie un peu de la structure désirée (parce que cela reste une simulation et une estimation de la structure spatiale). Mais ce n’est pas vraiment le cas ici. La figure 2 montre la structure spatiale du jeu de données simulé précédemment. Le pallier (pallier partiel + effet pépite) semble être un tout petit peu supérieur aux réglages. Pour autant, d’un point de vue général, la structure spatiale est bien respectée.

 

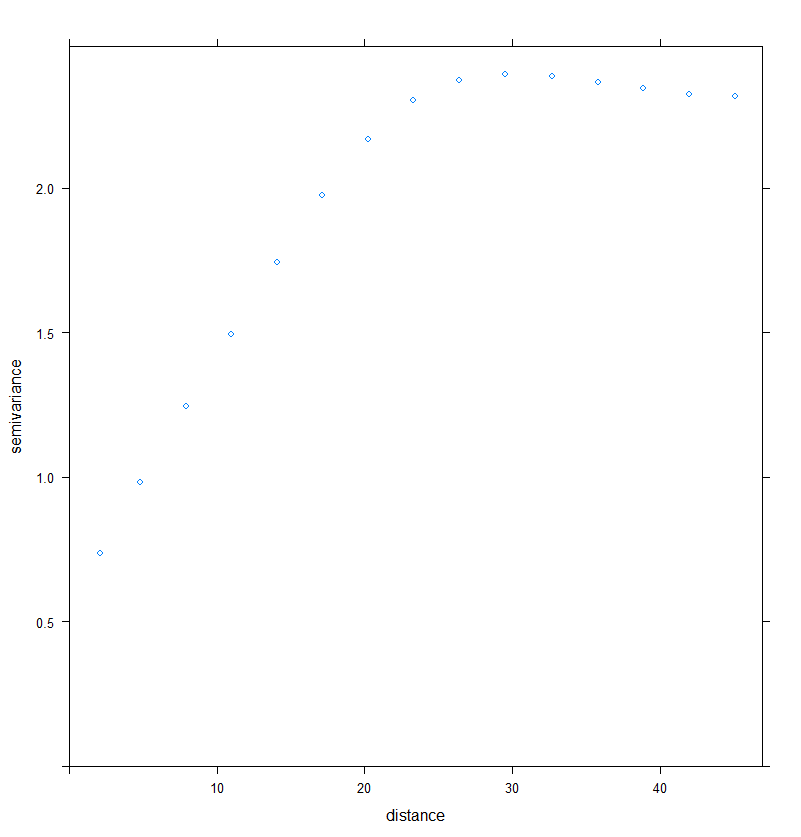
Figure 2. Structure spatiale du jeu de données simulé

---

Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

1. Bivand, R.S., Pebesma, E.J., & Gomez-Rubio, V. (2013) Applied Spatial Data Analysis with R. New York, NY: Springer