En Agriculture de Précision, on s’attache souvent à vouloir prédire les valeurs d’une variable d’intérêt. Plus que souvent, cette variable est coûteuse ou chronophage à acquérir et l’on cherche alors à développer un modèle plus ou moins complexe pour réussir à estimer correctement cette variable.

Par exemple, il est clair que les analyses de sol sont fastidieuses et relativement coûteuses. Pour pallier à ce problème, certains scientifiques travaillent sur des projets de spectroscopie du sol. L’objectif étant de mettre à profit des spectromètres pour développer des modèles spectraux et être capable de prédire certaines caractéristiques du sol (teneur en carbone ou potassium) par proxy-détection.

Pour que la prédiction soit précise, le modèle à mettre en place doit être validé sérieusement. L’objectif est de prouver que le modèle génère de bonnes estimations des valeurs de la variable étudiée. Pour ce faire, il est nécessaire de travailler au moins avec un jeu de données d’apprentissage et un jeu de données de validation. Assez simplement, les données d’apprentissage sont utilisées pour étalonner le modèle tandis que le jeu de validation sert à montrer que le modèle est fiable et pertinent. Pour être le plus objectif possible, les jeux de données d’apprentissage et de validation devraient être issus de population indépendante (pour être sûr de ne pas biaiser le résultat). D’une manière plus générale, ce qui est fait est de séparer un ensemble d’échantillons initial de base en un jeu de données d’apprentissage et un jeu de données de validation. A noter que s’il y a la possibilité d’acquérir deux jeux de données différents, un pour l’étalonnage et un autre pour la validation du modèle, il est recommandé de le faire ! Il est souvent conseillé d’utiliser entre 60 et 80% du jeu de données initial comme jeu d’apprentissage et les 20 à 40% restants comme jeu de validation. Néanmoins, ces pourcentages ne sont pas fixes.

Les indicateurs pour valider un modèle de prédiction

Une fois que le modèle a été créé avec le jeu de données d’apprentissage, il est nécessaire de calculer des indicateurs objectifs pour évaluer si le modèle a généré des prédictions pertinentes pour la variable étudiée. Les valeurs « vraies » de cette variable sont censées être connues pour l’ensemble des jeux de données d’apprentissage et de validation. Intuitivement, pour chaque échantillon dans le jeu de données de validation, on cherche à savoir si les valeurs prédites par le modèle sont proches des vraies valeurs du jeu de données de validation. Les indicateurs suivants sont les plus souvent reportés :

Le coefficient de determination : R²

R^{2}=1-\dfrac{\sum_{i=1}^{n}(y_i - \hat{y_i})^2}{\sum_{i=1}^{n}(y_i - \overline{y})^2}

Où n est le nombre de mesures, y_i est la valeur de la i^ème observation du jeu de données de validation, \overline{y} est la moyenne des valeurs du jeu de données de validation et \hat{y_i} est la valeur prédite pour la i^ème observation.

A noter que dans la précédente équation, la fraction est le ratio entre la somme des écarts résiduels et la somme des écarts totaux. Les résidus représentent les différences entre la prédiction et la réalité. Plus R² est proche de 1, meilleure est la prédiction. Dans un graphique à deux dimensions représentant les valeurs réelles en abscisse et les valeurs prédites en ordonnées, on cherche à ajuster une régression linéaire à l’ensemble des données (Fig. 1).

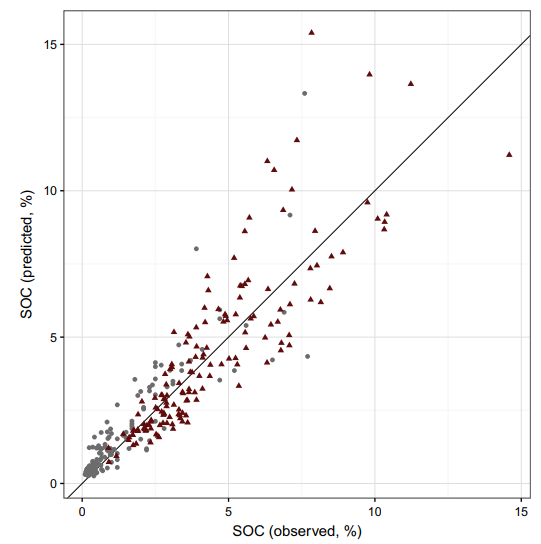
Figure 1. Ajustement de qualité entre les valeurs réelles et prédites. SOC est la teneur en carbone du sol (« Soil Organic Carbon content »)

Cependant, il est nécessaire de faire attention lorsque l’on calcule ce coefficient de détermination parce qu’il peut conduire à des conclusions erronées. En effet, certains points d’influence peuvent particulièrement augmenter la valeur du coefficient de détermination, ce qui peut parfois laisser penser que les prédictions sont assez précises. Ici, le modèle est relativement bien ajusté aux données. Les points gris proches de l’origine du graphique aident néanmoins à augmenter la valeur du coefficient de détermination.

Le biais

Le biais permet d’évaluer si les prédictions sont précises ou non et si le modèle a tendance à sur- ou sous-estimer les valeurs de la variable d’intérêt. Le biais se calcule comme suit :

Bias=\dfrac{\sum_{i=1}^{n}(\hat{y_i}-y_i)}{n}

Où y_i est la valeur de la i^ème observation du jeu de données de validation et \hat{y_i} est la valeur prédite pour la i^ème observation.

Plus le biais est faible (proche de 0), meilleure est la prédiction. Il faut faire attention au fait que cet indicateur ne prend pas en compte la variabilité des prédictions. En effet, si les valeurs prédites sont à la fois très sur-estimées mais aussi très sous-estimées, le biais peut quand même être relativement faible.

Pour évaluer visuellement si un modèle a tendance à sous- ou sur-estimer les valeurs d’une variable, il est possible d’afficher un graphique en deux dimensions comme précédemment mais en rajoutant la première bissectrice au graphique (la droite tracée sur la Figure 1). En fait, si les observations sont positionnés sur cette bissectrice, cela signifie que le modèle a généré une valeur égale à la valeur prédite. Si les observations sont en dessous de la ligne, les prédictions sont toujours inférieures aux valeurs réelles (les valeurs prédites sont sous-estimées). Le raisonnement contraire peut être appliqué si les observations sont au-dessus de la bissectrice.

L’erreur moyenne absolue : MAE

MAE=\dfrac{\sum_{i=1}^{n}\mid\hat{y_i}-y_i\mid}{n}

Où y_i est la valeur de la i^ème observation du jeu de données de validation et \hat{y_i} est la valeur prédite pour la i^ème observation.

La seule différence entre le MAE et le biais est la valeur absolue des différences entre les valeurs réelles et prédites. Un des avantages de l’indicateur MAE est qu’il donne une meilleure idée de la qualité de prédiction. Par contre, il n’est pas possible de savoir si le modèle a tendance à sous ou sur-estimer les prédictions.

L’erreur quadratique moyenne : RMSE

RMSE=\sqrt{\dfrac{\sum_{i=1}^{n}(\hat{y_i}-y_i)^2}{n}}

Un dernier indicateur pertinent est le RMSE. Cet indice fournit une indication par rapport à la dispersion ou la variabilité de la qualité de la prédiction. Le RMSE peut être relié à la variance du modèle. Souvent, les valeurs de RMSE sont difficiles à interpréter parce que l’on est pas en mesure de dire si une valeur de variance est faible ou forte. Pour pallier à cet effet, il est plus intéressant de normaliser le RMSE pour que cet indicateur soit exprimé comme un pourcentage de la valeur moyenne des observations. Cela peut être utilisé pour donner plus de sens à l’indicateur.

Par exemple, un RMSE de 10 est relativement faible si la moyenne des observations est de 500. Pourtant, un modèle a une variance forte s’il conduit à un RMSE de 10 alors que la moyenne des observations est de 15. En effet, dans le premier cas, la variance du modèle correspond à seulement 5% de la moyenne des observations alors que dans le second cas, la variance atteint plus de 65% de la moyenne des observations.

Aucun des indicateurs précédemment cités n’est clairement meilleur que les autres. Au contraire, toutes ces métriques sont à utiliser ensemble pour mieux comprendre et caractériser la qualité d’un modèle de prédiction.

Le compromis biais-variance

 

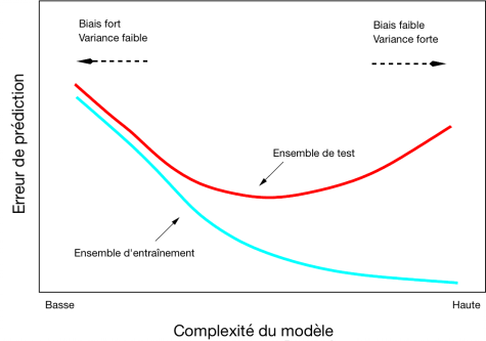
Figure 2. Le compromis biais-variance. Les jeux de données d’entrainement (ou apprentissage) et test (ou validation) sont présentés dans la section suivante « Les procédures de cross-validation »

La figure 2 illustre le compromis entre le biais et la variance d’un modèle. Sur cette figure, le biais se rapporte à l’exactitude du modèle (accuracy) et la variance peut être comprise comme la précision du modèle (precision). Lorsque l’on crée un modèle, l’objectif est d’avoir le biais et la variance les plus faibles possibles pour s’assurer des meilleures estimations. Cependant, il est relativement difficile de diminuer en même temps les deux paramètres. En effet, augmenter la variance revient à diminuer le biais. De la même façon, augmenter le biais conduit à une diminution de la variance.

Le biais et la variance sont en étroite relation avec la qualité d’ajustement du modèle aux données. Il peut être dit qu’un modèle avec une faible variance et un biais fort a tendance à être sous-ajusté aux données. En effet, cela veut dire que les prédictions ne seront pas très exactes (accuracy faible) mais que plusieurs réalisations du modèle conduiront à des estimations relativement cohérentes entre chaque réalisation. En d’autres mots, le modèle n’est pas spécifique aux données étudiées. Dans le cas contraire, un modèle avec une variance large et un biais faible est sur-ajusté aux données. Dans ce cas, le modèle est très spécifique aux données étudiées parce qu’il génère des prédictions très exactes (très proches de la réalité) pour ce jeu de données-là. Par contre, dès que le modèle sera appliqué dans une autre situation (sur un autre jeu de données par exemple), les estimations seront très mauvaises parce que le modèle n’aura pas la capacité de prendre en compte des observations trop différentes de celles qui auront servi à créer le modèle. Le sur-ajustement (Overfitting en anglais) est un problème relativement commun parce que les modèles sont souvent créés pour s’ajuster correctement aux données disponibles en amont pour construire le modèle. Quand le modèle est confronté à une source de données indépendantes, les résultats sont très peu fiables. C’est pourquoi il est fondamental d’étalonner un modèle avec un jeu de données d’apprentissage et de le valider avec un jeu de données de validation indépendant du jeu de données d’apprentissage. Les modèles devraient être assez souples pour être capable de prédire la valeur d’une observation qui n’est pas exactement similaire aux observations qui ont permis d’étalonner le modèle.

Les procédures de validation croisée (cross-validation)

Comme il l’a été expliqué précédemment, la validation d’un modèle de prédiction nécessite (i) de séparer un jeu de données initial en un jeu de données d’apprentissage et un jeu de données de validation, (ii) d’étalonner un modèle avec le jeu d’apprentissage et (iii) d’évaluer la qualité du modèle avec le jeu de données de validation en calculant les indicateurs définis préalablement. Pour s’assurer que la qualité du modèle soit bien mesurée, ces trois étapes doivent être répétées plusieurs fois. En effet, le jeu de données initial peut être séparé en un très grand nombre de paires de jeux de données d’apprentissage et de validation.

Par exemple, à la première itération, les 70% d’observations qui seront utilisés pour étalonner le modèle seront différents des 70% d’observations dans le jeu de données d’apprentissage de la seconde itération.

Les métriques de validation peuvent être moyennées sur toutes les itérations pour avoir une meilleure caractérisation du modèle. Ce concept est connu sous le nom de cross-validation parce que l’objectif est de savoir si la validation du modèle est équivalente lorsque différents jeux de données d’apprentissage et de validation sont utilisés. Au début du post, il a été dit que le jeu de données d’apprentissage était généralement composé de 60 à 80% des observations du jeu de données initial. Si le jeu de données de validation est réglé pour contenir 20% des observations et que plusieurs itérations sont réalisées, on dit que l’on a fait une 20-fold cross validation. Si le jeu de validation comprend seulement 5% des observations, c’est une 5-fold cross validation. Une autre méthode souvent reportée est la leave one out cross validation. Comme le nom le suggère, la validation est réalisée avec seulement une observation.

Valider un modèle de prédiction est nécessaire pour s’assurer que le modèle est effectivement capable de prédire avec précision et exactitude les valeurs d’une variable d’intérêt. Encore une fois, il faut bien comprendre que le modèle sera d’autant mieux évalué que les jeux de données d’apprentissage et de validation seront indépendants. Il arrive régulièrement que les personnes utilisent des jeux de données d’apprentissage et de validation très cohérents entre eux pour booster leurs indicateurs de validation (certains valident même leur modèle sur les données qui ont servi à étalonner leur modèle….). Il est recommandé de réaliser ces procédures de cross-validation et de calculer les indicateurs de validation pour que les modèles de prédiction soient correctement évalués.

Soutenez les articles de blog d’Aspexit sur TIPEEE

---

Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?