Le concept de logique floue a été proposé dans les années 60 par Lotfi Zadeh, un mathématicien et informaticien iranien, pour répondre aux limites de la bonne vieille logique classique. Mais alors de quelles limites parle-t-on ? Prenons un premier exemple très simple sur la température de l’eau qui coule lorsque l’on prend sa douche. Si on réfléchissait en logique classique, on réagirait de façon très binaire : l’eau est « froide » ou l’eau est « chaude ». C’est-à-dire qu’au fur et à mesure qu’on augmenterait la température de l’eau, on considérerait l’eau comme froide, puis froide, puis froide, puis instantanément, chaude. Vous, comme moi, réfléchissons de manière un peu différente (sinon prévenez-moi !), on aurait plutôt tendance à dire : l’eau est un « un peu moins froide », l’eau est « tiède », l’eau est « bientôt chaude » , etc. On voit déjà ici que l’ensemble des possibles est bien plus large que le premier ensemble binaire dont on a parlé. Pour continuer à appuyer mon propos, prenons un deuxième exemple très simple, celui de la vitesse à laquelle vous roulez en voiture sur l’autoroute. Si on raisonnait encore en logique classique, on pourrait dire par exemple : « Si je roule à moins de 100 km/h, je roule lentement et si je roule à plus de 100 km/h, je roule vite ». C’est un raisonnement un peu simpliste, vous en conviendrez… Ca voudrait dire qu’à partir du moment où vous dépassez les 100 km/h, tout d’un coup, vous vous mettez à rouler vite. Encore une fois, ce n’est pas de cette façon que réfléchit le cerveau humain, nous fonctionnons beaucoup plus par nuances, par transition, et c’est ce que la logique floue permet d’apporter. Dans ce dernier exemple, on dirait plutôt qu’on roule lentement sur l’autoroute en dessous de 70 km/h, qu’on roule vite au-dessus de 130 km/h, et qu’entre 70 et 130 km/h, on n’est ni lent, ni rapide, on est un peu des deux en quelque sorte.
Dans les deux exemples précédents, on a fait intervenir une seule variable (la température de l’eau dans le 1er cas et la vitesse sur l’autoroute dans le 2ème cas). Bien évidemment, il n’y a pas de limites sur le nombre de variables à utiliser pour prendre une décision, c’est d’ailleurs rare que l’on fasse un choix ou qu’on prenne une décision à partir d’une seule variable (on parle bien de décision multi-factorielle). Prenons un troisième exemple largement utilisé qui est celui du montant du pourboire que vous allez donner au serveur à la fin de votre repas au restaurant. Le montant de ce pourboire peut dépendre de la qualité du service, de la qualité de la nourriture, de votre humeur du jour, du moment que vous avez passé avec vos amis…. Si le service a été très bon, la nourriture moyenne et que vous êtes plutôt de bonne humeur, alors peut-être déciderez-vous de donner quand même un bon pourboire à ce serveur (qui n’a d’ailleurs pas grand-chose à voir avec la qualité de la nourriture qu’il vous sert).
Avant de rentrer plus dans le détail de la logique floue, on se rend compte que les trois exemples très simples qui ont été présentés ont permis d’aborder quelques concepts clés de la logique floue :
- En logique floue, une valeur peut appartenir à plusieurs ensembles à la fois contrairement à la logique classique. Par exemple, en reprenant notre exemple de vitesse sur l’autoroute, 90 km/h en logique classique, c’est une vitesse lente ; alors que 90km/h en logique floue, ce n’est pas totalement rapide mais ce n’est pas totalement lent non plus
- En logique floue (mais aussi en logique classique), on met en place un ensemble de règles (qu’on appellera règles d’inférence floue par la suite) de la forme « Si…., alors… ». Dans notre exemple de pourboire, on a par exemple donné une règle mais si on voulait modéliser complètement notre système de décision, il faudrait en rajouter d’autres ! (Par exemple si le service a été exécrable, que les plats étaient incroyables et que vous étiez de mauvaise humeur, alors le pourboire ne sera pas très élevé…).
- Dans les règles que j’ai choisies dans l’exemple du pourboire, j’ai mis en place des fonctions, notamment la fonction « ET ». Cela donne par exemple « Si le service a été très bon ET la nourriture moyenne ET je suis de bonne humeur, alors je donnerai un pourboire élevé ». La fonction « ET » en raisonnement logique s’interprète comme une intersection : pour que je donne un pourboire élevé, il faut qu’à la fois le service ait été très bon, que la nourriture moyenne et que je sois de bonne humeur. D’autres fonctions existent, comme nous allons le voir, notamment la fonction « ou » qui, en raisonnement logique, s’interprète plutôt comme une union : Si au moins un des deux critères est respecté (et pas nécessairement les deux comme avec une intersection), alors…
- Lorsque l’on utilise des variables au sein de nos règles, il faut être capable de donner une valeur ou de noter ces variables. Dans le cas de la température de l’eau ou de la vitesse sur l’autoroute, ça se comprend facilement puisqu’une température peut se mesurer en °C et qu’une vitesse peut se mesurer en km/h. Dans l’exemple du pourboire, ça veut dire qu’il faut que je sois capable de noter la qualité du service (par exemple entre 0 et 10) ou la qualité des plats (entre 0 et 10).
- Si on reprend l’exemple du pourboire, en plus de noter les variables, il va aussi falloir les interpréter pour pouvoir les prendre en compte dans le processus de décision. Depuis le départ, j’ai parlé de « très bon » service, « mauvaise » nourriture… mais à quoi est ce que ces « très bon » et « mauvais » correspondent ?
Allez, maintenant que ces premiers concepts ont été soulevés et qu’on a commencé à se poser quelques questions, voyons comment tout ça se met en place.
Les systèmes d’inférence floue
C’est vraiment une histoire de terminologie mais pour formaliser un peu tout ce qui a été évoqué plus haut, on parle plutôt de systèmes d’ « inférence floue » plutôt que de système de « logique floue ». Inférer, d’après notre ami Larousse, c’est tirer une conséquence de quelque chose, conclure, induire quelque chose de quelque chose. Inférer, c’est en gros ce qu’on essaye de faire ici : à partir d’un ensemble de variables et de règles, on prend une décision. D’où les systèmes d’inférence floue ! Et en anglais, la logique floue se dit « fuzzy logic » d’où tous les termes dérivés de « fuzzy » qu’on va voir par la suite.
Un système d’inférence floue est un système composé de trois grosses briques : la fuzzification, le moteur d’inférence et la défuzzification (Figure 1). Nous y reviendrons plus en détail juste après mais, pour en donner un aperçu, reprenons l’exemple du pourboire accordé à notre serveur. Les entrées de notre système d’inférence floue sont les notes que l’on va attribuer à chaque variable de notre prise de décision : la qualité de la nourriture, la qualité du service… Encore une fois, j’insiste sur le fait qu’il faut nécessairement que les variables soient quantifiables ou notables ! Admettons donc que nous avons noté la qualité de la nourriture et du service, chacune entre 0 et 10. Ces entrées sont dites « nettes » parce qu’elles sont très factuelles et très claires. On a par exemple donné 5.5/10 à la qualité de la nourriture et 7/10 à la qualité du service. Vient ensuite l’étape de fuzzification dans laquelle nous allons donner du sens ou interpréter les variables d’entrée de notre modèle de décision. Il faudra donc expliciter, pour chaque variable dans son intervalle de valeur, les différents états qu’elle peut prendre. C’est ici que l’on définira jusqu’à quelle note la nourriture est considérée comme mauvaise, à partir de quand elle sera considérée comme moyenne… J’en profite pour vous rappeler ici qu’on a vu qu’une valeur pouvait être dans plusieurs ensembles ou plusieurs états en même temps (nldr : l’exemple de la vitesse en voiture). En faisant passer nos variables d’entrée dans ce système flou, on obtient alors des variables d’entrée que l’on va considérer comme floues elles aussi. Le moteur d’inférence, c’est l’étape dans laquelle on va paramétrer nos règles de décision « Si…, alors… ». Grâce à ce moteur, on va pouvoir appliquer les règles que l’on a fixées à nos variables d’entrée floues. La dernière brique du système d’inférence floue, c’est la défuzzification dont l’objectif est de synthétiser le résultat de notre décision multi-factorielle. Hé oui, dans notre exemple de pourboire, on veut savoir combien on va devoir donner au serveur, donc il nous faut une valeur de sortie claire et nette : un montant en espèces sonnantes et trébuchantes ! Allez, on entre dans le détail de ces différentes briques, suivez le guide !
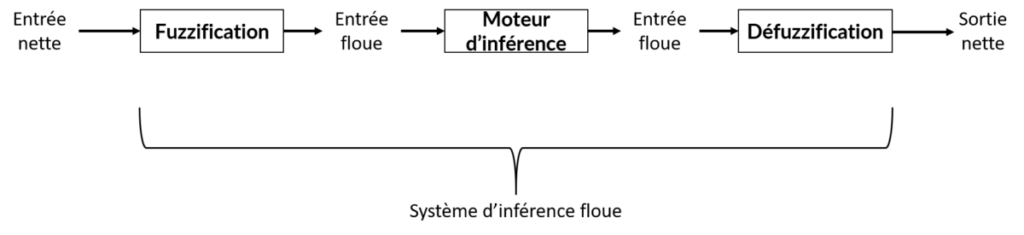
Figure 1. Système d’inférence floue
Un exemple un peu plus agro
Et si on repartait d’un exemple avec un peu plus d’attrait pour l’agronomie ? Les exemples présentés plus haut sont très parlants, certes, mais dans cette communauté, on essaye quand même d’appliquer des méthodes de Data Science à des problématiques agro-environnementales. Imaginons un problème très simple où nous chercherions à construire un système d’inférence floue pour faire de la prédiction de rendement à la parcelle dans une région géographique donnée à partir de deux variables d’entrée : le potentiel du sol (noté entre 0 et 10 à partir d’une expertise terrain par un pédologue) et les précipitations totales sur l’année (entre 0 et 1000 mm). Cet exemple est très simpliste et ne sert que de démonstration aux principes de la logique floue.
Fuzzification
La fuzzification est l’étape où l’on va apporter de l’expertise sur nos variables d’entrée, c’est-à-dire que l’on va découper nos variables d’entrée en différentes classes qui ont du sens pour nous. Pour faire ça, il va falloir définir ce que l’on appelle des fonctions d’appartenance (Figure 2).
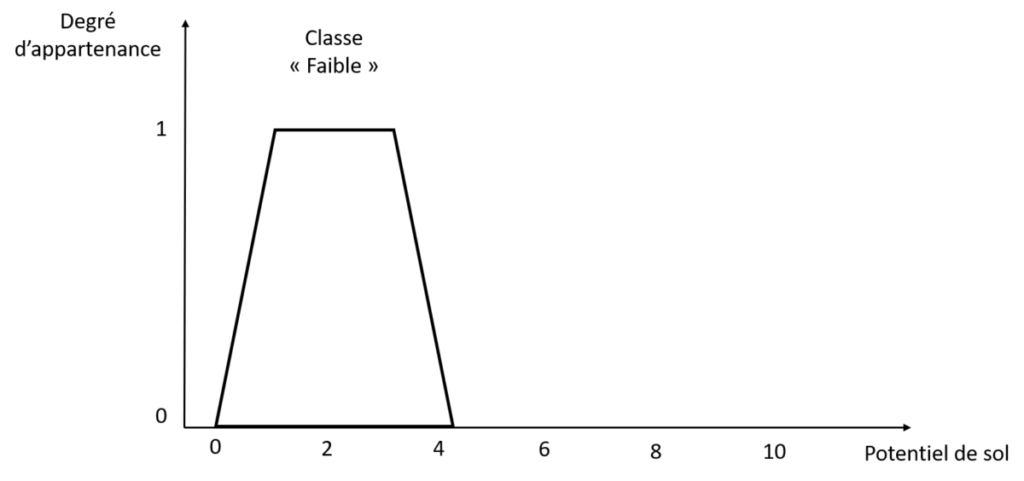
Figure 2. Fonction d’appartenance du sous ensemble « Faible » de la variable Potentiel de sol
La fonction d’appartenance est définie pour chacun des sous-ensembles (ou classes) de chaque variable. Elle est définie sur un intervalle de valeur (entre 0 et un peu plus de 4 pour la classe « Faible » sur la figure 2) compris dans l’intervalle de valeur de la variable à laquelle elle correspond (entre 0 et 10 pour le potentiel de sol). Encore une fois, cette fonction est définie de manière experte ! C’est nous qui la choisissons !
La fonction d’appartenance prend ses valeurs entre 0 et 1. Il est possible que vous voyiez des fonctions d’appartenance avec des valeurs supérieures à 1 mais ça reste rare, il est quand même beaucoup plus facile de travailler avec des valeurs normalisées entre 0 et 1. Nous allons donc exclusivement travailler avec des degrés d’appartenance à la fonction d’appartenance (l’axe des ordonnées) compris entre 0 et 1. Ces degrés d’appartenance sont généralement notés /mu. La fonction d’appartenance définie dans la figure 2 a une forme trapézoidale. C’est un choix que j’ai fait ici mais on pourrait en imaginer plein d’autres (Figure 3). Ces fonctions peuvent prendre la forme que vous voulez, si tant est que cette forme ait un sens pour la variable que vous cherchez à expliciter.
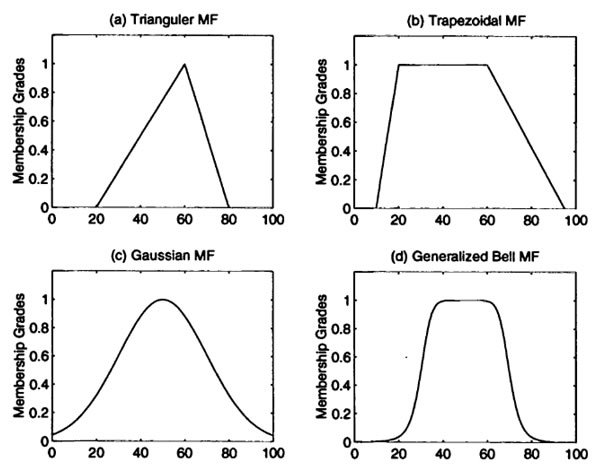
Figure 3. Exemples de fonctions d’appartenance
Alors, comment lit-on la fonction d’appartenance qui est présentée sur la figure 2 ? Je vous invite pour ça à regarder la figure 4 dans laquelle je choisis quelques exemples au hasard de valeurs de potentiel de sol. Si le potentiel de sol de ma parcelle a une note de 0.5, cela veut dire que je considère qu’il appartient à 60% à la classe « Faible » de la variable Potentiel de sol. Si le potentiel est de 3.5, il appartient à 80% à la classe « Faible ». Et si le potentiel est à 7 ? Et bien, il appartient à 0% à la classe « Faible ».
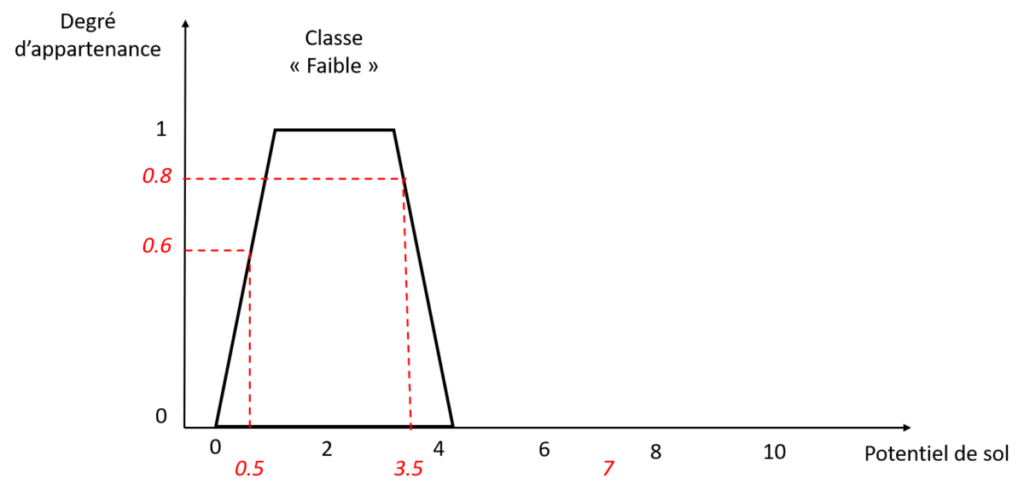
Figure 4. Lecture et compréhension de la fonction d’appartenance
Comment comprendre alors un potentiel de sol avec une valeur de 7 ? C’est tout simplement qu’ici, nous n’avons défini que la fonction d’appartenance de la classe « Faible », nous n’avons pas caractérisé l’ensemble de la variable Potentiel de sol ! C’est ce que nous allons faire par la suite mais juste avant, laissez-moi définir quelques termes liés à la fonction d’appartenance (Figure 5).
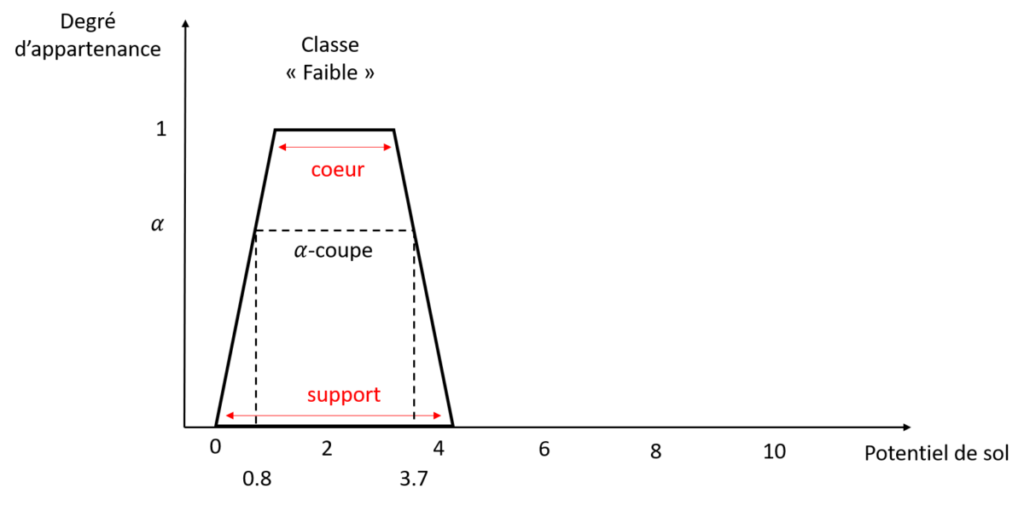
Figure 5. Terminologies de la fonction d’appartenance
Une fonction d’appartenance est définie par deux paramètres principaux. Tout d’abord, son support (le nom est le même en anglais) : c’est l’ensemble des valeurs pour lesquelles vous allez considérez qu’elles appartiennent au moins en partie à la classe étudiée. Ici, les valeurs comprises entre 0 et 4.2 appartiennent à la classe « Faible » avec un degré d’appartenance supérieur à 0. Ensuite le cœur ou noyau (vous trouverez les termes core ou kernel en anglais): c’est l’intervalle de valeurs pour lesquelles vous considérez que les valeurs appartiennent entièrement à la classe que vous étudiez, et à aucune autre classe. Sur la figure 5, si le potentiel de sol est compris entre 1 et 3.5, alors ce potentiel de sol appartient à la classe « Faible » avec un degré d’appartenance de 100% [Et dans le cas d’une fonction d’appartenance triangulaire, cet intervalle n’est en fait qu’une seule valeur, la pointe du triangle – Figure 3]. Euh, minute papillon !! En gros, t’es en train de me dire qu’un potentiel de sol de 1.5, ça appartient à 100% à la classe « Faible » mais qu’un potentiel de sol de 0.5, ça n’appartient qu’à 60% à la classe « Faible » ? C’est pas un peu bizarre tout ça ? C’est vrai que vu comme ça, ça pose question. En fait, vu comme on a défini la classe « Faible » du potentiel de sol, c’est comme ça que ça s’interprète. Il y a deux manières de voir les choses. Soit ça laisse penser qu’on aurait pu définir une classe « Très faible » pour le potentiel de sol. Soit, si on considère qu’un potentiel de sol, c’est forcément supérieur à 0, hé bien on peut redéfinir la fonction d’appartenance associée à la classe « Faible » du potentiel de sol comme sur la figure 6. Ca vous va mieux ?
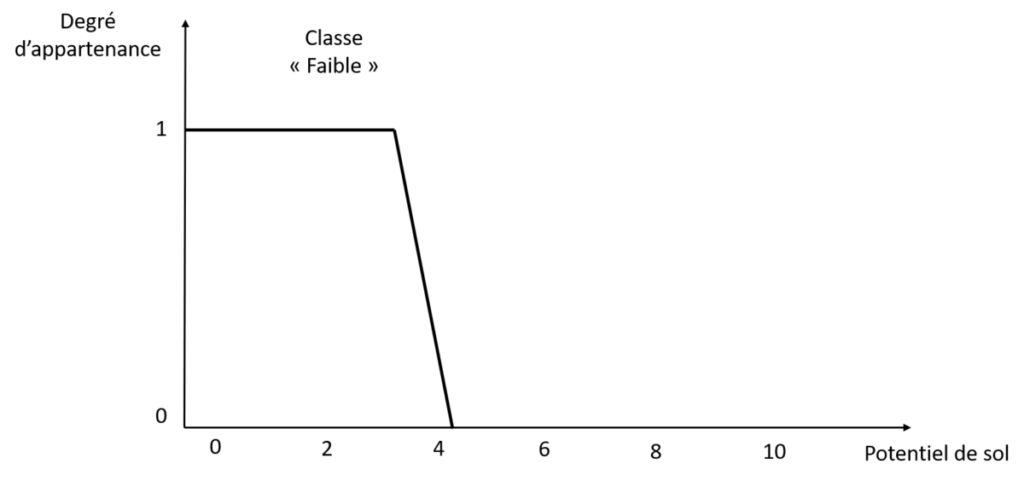
Figure 6. Redéfinition de la fonction d’appartenance à la classe « Faible » du potentiel de sol.
Et le dernier terme présenté sur la figure 5 : une alpha-coupe, c’est l’intervalle de valeurs pour lesquelles les valeurs ont un degré d’appartenance à la classe étudiée supérieure à alpha. Par exemple, sur la figure 5, une 0.6-coupe, c’est l’intervalle de valeurs compris entre 0.5 et 3.7.
Voilà, il ne nous reste plus qu’à reprendre le travail qu’on vient de faire pour toutes les classes de potentiel de sol que l’on souhaite définir. J’ai par exemple défini 3 classes de potentiel de sol, et donc dessiné 3 fonctions d’appartenance à la variable potentiel de sol (Figure 7). L’ensemble défini sur l’intervalle [0-10] composé de ces trois fonctions d’appartenance, pour la variable potentiel de sol s’appelle la variable linguistique potentiel de sol.
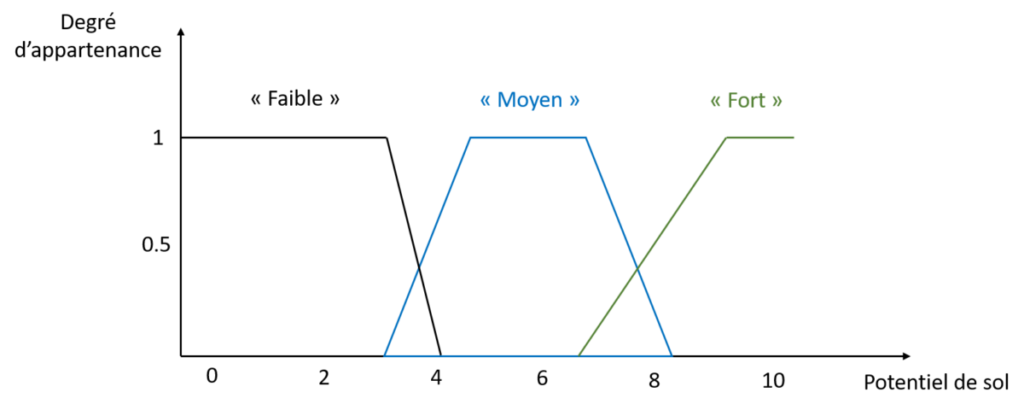
Figure 7. Variable linguistique Potentiel de sol.
On comprend bien sur ce graphique que certaines valeurs ont des degrés d’appartenance définis pour plusieurs classes. Par exemple, un potentiel de 7 a un degré d’appartenance de 0 à la classe « Faible », 0.7 à la classe « Moyenne » et 0.2 à la classe « Forte ». La somme des degrés d’appartenance d’une valeur n’a pas besoin d’être égale à 1, ce n’est pas obligatoire. Et il n’est pas obligatoire non plus d’avoir des fonctions d’appartenance qui se croisent, on peut très bien imaginer des fonctions d’appartenance bien séparées sur l’intervalle de valeurs possibles. Encore une fois, tout dépend de l’expertise que vous avez sur vos variables et de la façon dont vous les interprétez.
Rappelez-vous, nous voulons mettre en place un système d’inférence floue pour inférer un rendement en fonction de deux variables d’entrée, le potentiel de sol et la pluviométrie de l’année. Il faut donc que je définisse encore mes variables linguistiques « Pluviométrie » et « Rendement » (il faut aussi définir une variable linguistique pour notre variable de sortie, le rendement, et nous verrons pourquoi par la suite !). C’est chose faite sur la figure ci-dessous. Ce que vous voyez ici, ce sont mes choix, que je vous propose à titre d’exemple pour appuyer mon propos.
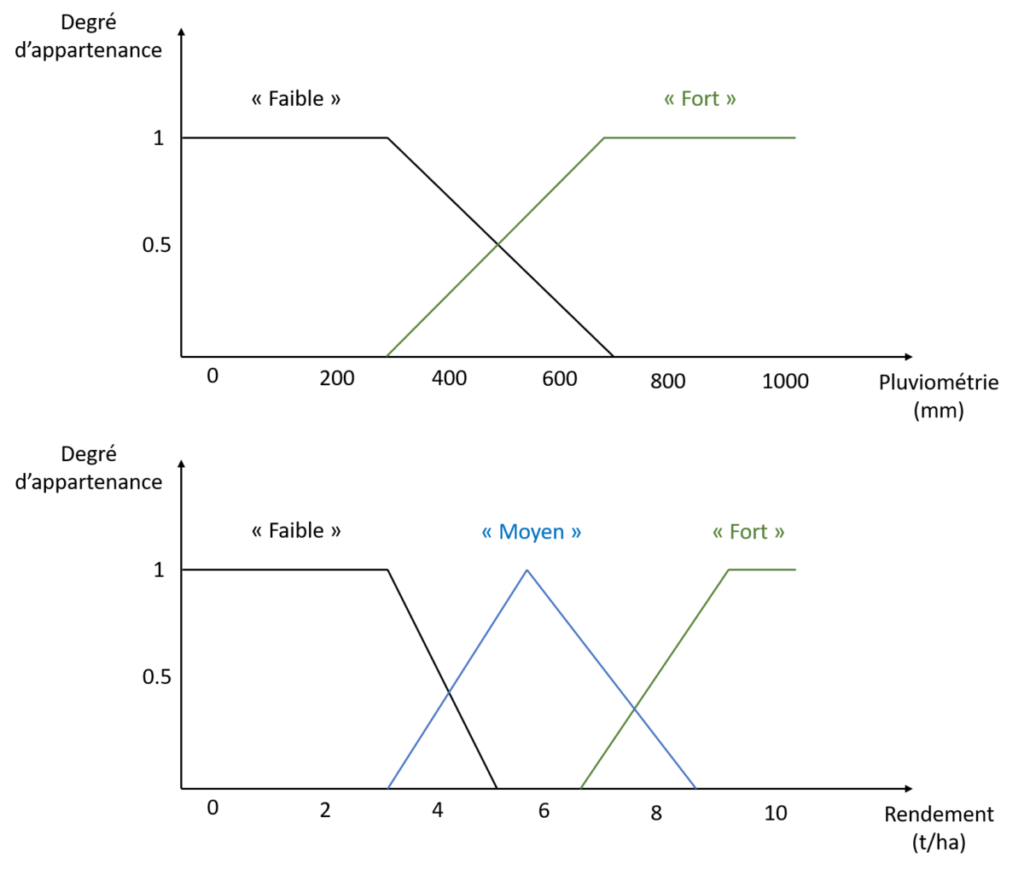
Figure 8. Variables linguistiques Pluviométrie et Rendement.
Moteur d’inférence
On a déjà défini des fonctions d’appartenance pour les variables qui nous intéressent, c’est déjà pas mal ! Maintenant, comme on l’a vu en introduction, il nous faut définir des règles ! Ces règles vont expliciter comment se comportera le rendement en fonction de nos variables de potentiel de sol et de pluviométrie. Au risque de me répéter encore, dans notre exemple, ces règles sont définies de manière experte ! Nous verrons qu’on peut aussi inférer des règles mais ce n’est pas notre objectif ici. Nous pouvons donc imaginer que nous avons mis en place des expérimentations et que l’on veut construire un système d’inférence floue pour formaliser nos expérimentations et nos résultats. Ce système sera ensuite utilisé pour faire par exemple de nouvelles prédictions lorsque l’on aura de nouvelles données. Imaginons donc que je définisse les règles suivantes :
- Règle 1 : Si le potentiel de sol est fort OU la pluviométrie est forte alors le rendement est fort
- Règle 2 : Si le potentiel de sol est moyen, alors le rendement est moyen
- Règle 3 : Si le potentiel de sol est faible ET la pluviométrie est faible, alors le rendement est faible
On appelle règle incomplète, une règle qui n’utilise pas l’ensemble des variables d’entrée. C’est par exemple le cas de la règle 2. Et ce n’est pas grave ! En tant qu’experts, on ne raisonne pas forcément avec l’ensemble de nos variables d’entrée à chaque fois. Et il n’est pas non plus obligatoire d’avoir une règle pour chaque cas de figures envisagé ! Ca peut être bien si on veut un modèle complet mais si on ne veut pas un modèle trop spécifique à nos données non plus, il faut être relativement flexible et ne pas incorporer trop de règles.
Dans ces règles, on observe qu’on a le classique « Si…, alors… » mais que pour les règles 1 et 3, il y a aussi deux fonctions : « OU », « ET ». Comment donc interpréter ces fonctions là dans notre système d’inférence floue. Si je dispose de valeurs d’entrée de potentiel de sol et de pluviométrie, comment est ce que je peux travailler avec ces règles-là ? En introduction, on avait commencé à essayer de sentir ce que ces fonctions « OU » et « ET » voulaient dire et on les avait notamment rapprochées respectivement de notions de « réunion » et d’ « intersections » d’intervalles. Pour que la règle 1 s’active ou se réalise, il faut qu’on ait soit un potentiel de sol fort, soit une pluviométrie forte. Mais on n’a pas besoin des deux, seule l’une des deux conditions suffit à activer la règle (c’est le « OU »). Pour que la règle 3 s’active ou se réalise, il faut qu’on ait la fois un potentiel de sol faible et une pluviométrie faible. On a donc besoin des deux conditions pour que la règle se réalise (c’est le « ET »). Une fois que l’on a bien compris la différence entre ces deux fonctions, présentons maintenant deux types d’opérateurs pour les prendre en compte :
- Les opérateurs de Zadeh (du nom de Lotfi Zadeh) :
- Synthétisent la notion de réunion (c’est la fonction « OU ») par le maximum des degrés d’appartenances aux classes considérées
- Synthétisent la notion d’intersection (c’est la fonction « ET ») par le minimum des degrés d’appartenances aux classes considérées
Montrons par l’exemple ce qui se passe avec la règle 1. La règle 1 s’active si et seulement si le potentiel de sol est fort OU la pluviométrie est forte. Imaginons que j’ai un potentiel de sol « fort », disons 8, et une pluviométrie « forte », disons 600mm (Figure 9).
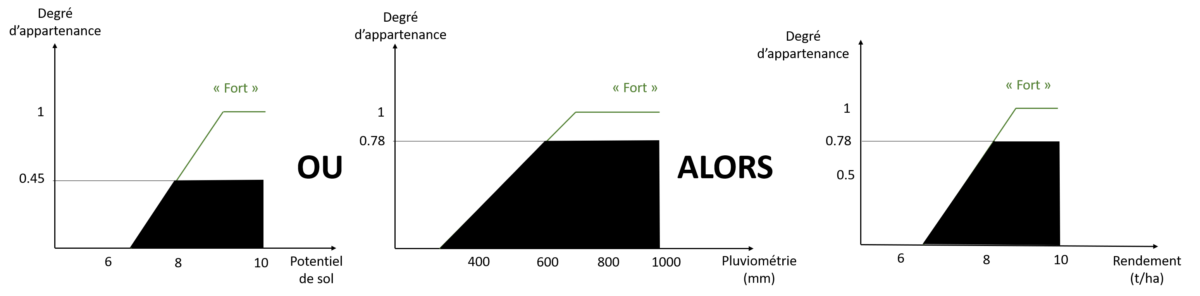
Figure 9. Activation de la règle n°1 de notre système d’inférence floue
Si la règle 1 est activée, alors le rendement est fort, c’est ce qu’on voit sur la figure. Et le degré d’appartenance correspondant est le maximum des degrés d’appartenance de nos valeurs d’entrée aux classes fortes de potentiel de sol et de pluviométrie. Si, dans la règle 1, nous avions eu la fonction « ET » à la place de la fonction « OU », le degré d’appartenance finale à la classe forte de rendement aurait été 0.45 et pas 0.78, puisqu’on aurait appliqué le minimum des degrés d’appartenance. Dans cet exemple, on regarde l’appartenance à la classe de rendement « Forte » simplement parce que c’est ce que nous dit la règle 1 ! Si j’avais défini la règle « Si le potentiel de sol est fort OU la pluviométrie est forte, alors le rendement est moyen », j’aurais obtenu la figure suivante :

Figure 10. Autre exemple d’activation de règles
Et je ne me serais pas intéressé aux classes de potentiel de sol « faible » et « moyen », ni à la classe de pluviométrie « faible » même si elles se chevauchaient, tout simplement parce que la règle 1 ne les mentionne pas !
- Les deuxièmes types d’opérateurs sont les opérateurs dits probabilistes, ils :
- Synthétisent la notion de réunion (c’est la fonction « OU ») par la somme des degrés d’appartenances aux classes considérées moins le produit des degrés d’appartenances aux classes considérées
- Synthétisent la notion d’intersection (c’est la fonction « ET ») par le produit des degrés d’appartenances aux classes considérées
Si on reprend l’exemple donné en figure 9 :
- En utilisant les opérateurs de Zadeh, en activant la règle 1 avec notre exemple, le degré d’appartenance à la classe de rendement « Fort » était de 0.78. C’était le maximum des degrés d’appartenances : max (0.45 ; 0.78)
- En utilisant l’opérateur probabiliste de la même façon, on aurait obtenu le degré d’appartenance 0.45+0.78 – 0.45×0.78 = 0.879
Le choix de l’opérateur a donc de l’influence sur le degré d’appartenance obtenu en sortie ! Chaque utilisateur choisira le type d’opérateurs qui sera le plus en accord avec son expertise. On se rend compte que l’opérateur de Zadeh est un peu plus brutal dans le sens où un seul des degrés d’appartenance d’entrée est utilisé pour calculer le degré d’appartenance en sortie. Avec les opérateurs probabilistes, il y a un peu plus l’idée d’un compromis puisque la totalité des degrés d’appartenances d’entrée sont utilisés.
Dans notre exemple d’inférence de rendement, nous avons défini 3 règles (règles n°1 à 3). Pour un nouveau couple de donnée d’entrée (Potentiel de sol ; Pluviométrie), on va pouvoir inférer un rendement en fonction de l’activation ou non des règles que l’on a fixées. Comme on l’a vu dans les figures 9 et 10, lorsqu’une règle est activée, on obtient un ensemble flou en sortie (c’est l’espèce de masse noire dessinée sur les figures). Comment faire lorsque plusieurs règles s’activent en même temps ? En d’autres termes, comment combiner le résultat de ces règles ? Et surtout, au vu de notre problématique initiale, comment caractériser le rendement en sortie de notre modèle d’inférence, c’est-à-dire quelle sera la valeur de rendement attendue ? On va voir tout ça dans la dernière brique des systèmes d’inférence floue : la défuzzification.
La défuzzification
Pour bien comprendre ce à quoi on fait face, considérons que l’on a mis en place notre système d’inférence floue. Nous avons donc un ensemble de variables linguistiques (celles que nous avons définies plus haut) et un ensemble de règles associées (ce sont les règles 1, 2 et 3 de la section précédente). On peut maintenant inférer un rendement à partir d’un couple de valeurs de potentiel de sol et de pluviométrie. Voyons ce qui se passe. Imaginons que lors d’une nouvelle expérimentation au champ, nous mesurions sur une parcelle un potentiel de sol de 7 et une pluviométrie de 500mm.
D’après notre variable linguistique Potentiel de sol, on se rend compte qu’une valeur de 7 correspond à un degré d’appartenance de 0 à la classe « faible », de 0.7 à la classe « moyenne » et de « 0.2 » à la classe « forte ». De la même façon, d’après notre variable linguistique Pluviométrie, on se rend compte qu’une valeur de 500mm correspond à un degré d’appartenance de 0.5 à la classe « faible », et de 0.5 à la classe « forte ». En suivant les règles d’inférence floues que l’on a définies, on observe que :
- la règle 1 s’active parce que la condition potentiel de sol « forte » OU pluviométrie « forte » est respectée
- la règle 2 s’active parce que la condition potentiel de sol « moyen » est respectée (le degré d’appartenance correspondant est supérieur à 0, il est de 0.7)
- la règle 3 ne s’active pas parce que le degré d’appartenance à la classe « faible » de l’ensemble Potentiel de sol est de 0 et que le degré d’appartenance à la classe « faible » de l’ensemble Pluviométrie est de 0.5. Il faut que les deux conditions soient respectées pour que la règle s’active au vu de la fonction « ET » de la règle.
Graphiquement, on a donc la figure suivante pour ces trois règles :
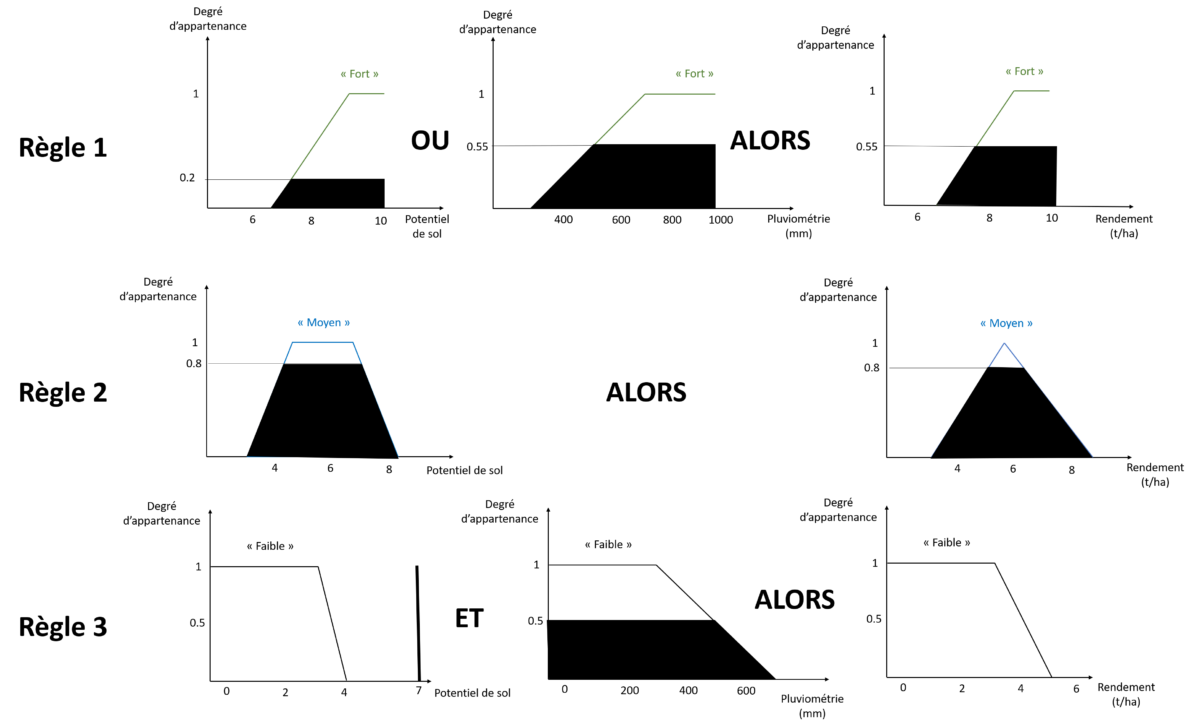
Figure 11. Inférence de rendement à partir de nouvelles données d’entrée et des règles d’inférence définies
En combinant les trois sorties, on arrive à l’inférence complète suivante :
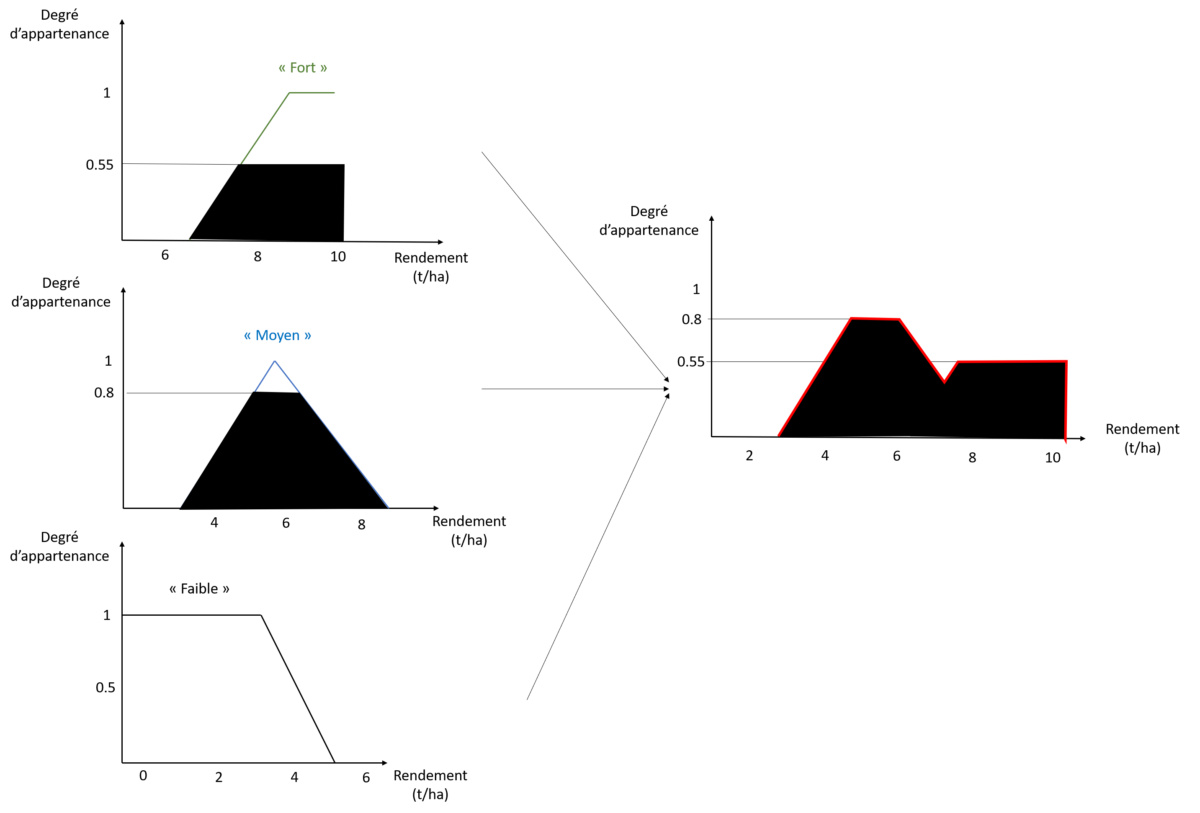
Figure 12. Combinaison des sorties de rendement pour le couple de Potentiel de sol ; Pluviométrie (7 ; 500). Faites bien attention aux valeurs en abscisse.
Comme discuté plus haut, l’étape de défuzzification va consister à transformer l’ensemble flou de rendement en une valeur finale nette de rendement pour notre couple de Potentiel de sol ; Pluviométrie (7 ; 500). Plusieurs méthodes de défuzzification existent mais je n’en présenterai que deux, qui sont celles principalement connues.
- La première est la méthode moyenne des maximas (MM). Dans cette méthode, la sortie est calculée comme la moyenne des abscisses pour lesquels le degré d’appartenance est maximal. Dans l’exemple de la figure 12, on regarde donc le degré d’appartenance maximal (0.8) et les valeurs de rendement en abscisses correspondantes (l’intervalle [5-6.5]). Le rendement final est obtenu en calculant la moyenne de l’intervalle, soit (5+6.5)/2=5.75 t/ha
- La deuxième méthode est celle du centre de gravité (COG pour Center Of Gravity). Dans cette méthode, la sortie est calculée comme l’abscisse du centre de gravité de la surface sous la courbe (la courbe rouge), ici autour de 6.2 t/ha.
Comme pour les opérateurs, on se rend compte que la méthode de défuzzification impacte la sortie finale nette du système d’inférence floue. C’est à l’utilisateur de choisir la méthode la plus appropriée selon lui. La méthode des maximas est assez brutale, seul le degré d’appartenance maximal est considéré. La méthode du centre de gravité est plus flexible puisque l’ensemble de la sortie floue est pris en compte pour calculer la sortie de défuzzification. On peut voir cette méthode comme une sorte d’interpolation. Elle est néanmoins plus gourmande en temps de calcul, c’est normal puisqu’il lui faut calculer un centre de gravité.
En guise de discussion et de conclusion
Après avoir construit un système d’inférence floue (mise en place des fonctions d’appartenance, établissement des règles d’inférence floues, défuzzification des sorties floues du système), on est donc capables d’inférer une valeur de sortie de rendement à partir de nouvelles valeurs d’entrée de potentiel de sol et de pluviométrie. Si on essaye de prendre un peu de recul, quels sont les gros avantages des systèmes d’inférence floues ?
- On peut incorporer de l’expertise dans son modèle grâce aux fonctions d’appartenance et aux règles d’inférence !
- On peut modéliser des phénomènes non linéaires ! Aucune de nos fonctions d’appartenance ni de nos règles n’avait de comportement linéaire. On peut donc modéliser des phénomènes complexes.
- On peut jouer sur le flou et l’incertitude de nos données avec les fonctions d’appartenance. Imaginez par exemple que vous connaissiez l’incertitude de mesure de votre capteur. Vous pouvez par exemple modéliser les données que vous collectez avec une fonction d’appartenance. Vous n’avez alors pas une seule valeur en sortie du capteur mais bien un ensemble de valeurs avec un degré d’appartenance donné par votre fonction d’appartenance. On peut aussi imaginer travailler en deux dimensions avec l’incertitude associée au positionnement d’un engin agricole dans l’espace (Figure 13). On définit alors de la même façon un noyau et un support mais en deux dimensions.
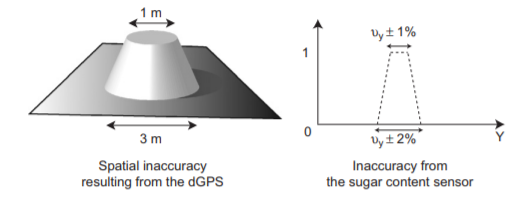
Figure 13. Prise en compte de l’incertitude associée au positionnement d’une machine agricole dans l’espace (gauche) et à l’incertitude associée à la mesure de teneur en sucre d’une baie par un capteur (droite). Tiré de Paoli et al., (2007). Spatial Data Fusion for Qualitative Estimation of Fuzzy Request Zones : Application on Precision Viticulture. Fuzzy Sets and Systems, 158, 535-554.
Dans tout ce post de blog, je suis parti du principe que l’on avait l’expertise requise pour générer les règles d’inférence floue. C’est-à-dire que j’ai considéré que l’on avait travaillé de façon dite « supervisée ». On a des données d’entrée, on construit des fonctions d’appartenance, on connait les règles de notre système d’inférence floue et on utilise ce système pour produire des estimations. Néanmoins, il est possible de travailler avec de la logique floue de façon « non supervisée ». Dans ce cas-là, à partir des fonctions d’appartenance que l’on définit (on est obligés d’en définir par contre, les modèles d’apprentissage non supervisées ne peuvent pas les inventer puisque c’est notre expertise), le modèle peut trouver les règles les plus adéquates à notre système d’inférence floue. Le problème que l’on peut avoir en travaillant de cette façon-là, c’est que notre modèle peut générer énormément de règles ce qui peut rendre la compréhension du système relativement complexe… Néanmoins, certains algorithmes existent pour tenter ensuite d’optimiser ou de simplifier les règles générées de manière à clarifier le système d’inférence floue. On comprend bien que si on génère un tas de règles et que personne n’est capable de les interpréter, ça n’a pas vraiment d’intérêt… Encore une fois, l’objectif n’est pas d’aboutir à un trop grand nombre de règles, sinon le modèle ne sera pas utilisable ni généralisable à d’autres données que celles qui ont permis de le construire (c’est toujours le même problème de sur-apprentissage).
Pour travailler sur des aspects de logique floue, plusieurs options s’offrent à vous mais je vous conseille, pour vous y atteler, de commencer par le logiciel FisPRO (https://www7.inra.fr/mia/M/fispro/fispro2013_en.html) développé par une équipe de l’INRA et qui propose une interface assez facile à manipuler pour mettre en place des systèmes d’inférence floue.

Un dernier point d’attention : J’espère avoir été assez clair sur le fait que les variables d’entrée que l’on utilise dans un système d’inférence floue doivent être quantifiables ou notables sur une échelle (il faut des valeurs numériques). Le point que je soulève ici fait référence à l’usage de variables absolues ou relatives. En agro-environnement, si vous en venez à utiliser une variable telle que l’altitude ou la conductivité, il faudra toujours se référer à un contexte en particulier. Par exemple, dire qu’une altitude est faible ou forte n’a pas vraiment de sens. Une altitude forte à un endroit est peut-être considérée comme faible à une autre. Il est donc parfois peut-être plus intéressant de travailler de manière relative plutôt qu’absolue, en raisonnant par exemple, si vous travaillez avec un jeu de données intra-parcellaires, avec les valeurs d’altitude par rapport à l’altitude moyenne de la parcelle plutôt qu’avec les valeurs d’altitudes brutes telles quelles.
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

