Rares sont ceux qui vous diront que leurs données sont toutes jolies et toutes propres et qu’elles peuvent être utilisées telles quelles dans des modèles décisionnels… C’est un fait. Lorsqu’un jeu de données est collecté, personne n’est à l’abri que des données biaisées ou aberrantes viennent s’ajouter à la fête et perturber la qualité des données ainsi acquises. Et des sources d’erreurs, il n’en manque pas ! Problème de fonctionnement d’un capteur, Manque d’expertise d’un opérateur, Mauvais support de mesure utilisé… Dans cet article, on va tenter de faire ami-ami avec les données aberrantes, histoire de voir un peu plus en détail à quoi elles ressemblent et comment les caractériser. Tout ça dans l’objectif de pouvoir s’en occuper par la suite (mais ça, il ne faut pas leur dire !). Allez, c’est parti.
Données aberrantes, présentez-vous !
Une anomalie ou une valeur aberrante peut être décrite comme une observation qui s’écarte tellement du reste des observations que l’on peut soupçonner qu’elle ait été produite par un mécanisme différent (Hawkins, 1980). Ces valeurs aberrantes peuvent être attribuées à quantités de processus, par exemple à une erreur de mesure ou à des phénomènes spécifiques, par exemple l’apparition d’un incendie ou d’un événement climatique (Chandola et al., 2009). La détection des valeurs aberrantes est l’un des principaux domaines d’investigation de la communauté du Data Mining. L’identification des valeurs aberrantes s’est étendue à de nombreuses applications telles que la détection des fraudes, les réseaux de trafic ou la surveillance militaire. Par exemple, dans le cas des données de rendement intra-parcellaires (c’était le sujet de ma thèse), il a été démontré à plusieurs reprises comment les valeurs aberrantes – même en quantité limitée – pourraient affecter la qualité de l’ensemble d’un jeu de données (Griffin et al., 2008 ; Taylor et al., 2007). Ce qui est intéressant de noter, c’est que selon le domaine d’application, certains vont chercher à supprimer les valeurs aberrantes de leurs jeux de données (parce qu’elles vont en perturber la qualité et la pertinence) tandis que d’autres peuvent, au contraire, avoir un intérêt particulier à trouver et à détecter les valeurs aberrantes pour mettre en évidence un phénomène (une forte hausse des températures peut par exemple être le signe d’un incendie naissant).
Les valeurs aberrantes peuvent être décrites de plusieurs façons : (i) les valeurs aberrantes locales ou globales, (ii) les valeurs aberrantes ponctuelles, contextuelles ou régionales, et (iii) les valeurs aberrantes univariées ou multivariées. Les valeurs aberrantes globales sont les typologies les plus simples à identifier. Il s’agit souvent de données qui ont un comportement vraiment spécifique, très différent de celui de l’ensemble du jeu de données, c’est-à-dire que ces valeurs aberrantes sont toujours éloignées de la distribution générale de l’ensemble de données. Les valeurs aberrantes locales sont plus profondément enracinées dans les ensembles de données. Leur comportement n’est pas atypique par rapport à l’ensemble de la distribution, ce qui ne permet pas une identification simple. Cependant, ces valeurs aberrantes sont suspectes à l’égard de leur voisinage (Chandola et al., 2009). La détection de ces valeurs aberrantes nécessite de définir des relations de voisinage entre les données afin de limiter la recherche à un sous-ensemble de voisins plutôt qu’à l’ensemble des données. Pour les observations non spatialisées (non localisées dans l’espace), les relations de voisinage entre observations dépendent de la proximité d’attributs non spatiaux. Pour les données spatiales, ces relations de voisinage dépendent de la proximité dans l’espace d’une observation à ces voisins (Cai et al., 2013 ; Chawla et Sun, 2005). La figure 1 présente le comportement d’outliers locaux et globaux dans un jeu de données spatialisées (à gauche, on regarde les attributs non spatiaux, et à droite on regarde la proximité des observations dans l’espace avec leurs coordonnées). On peut distinguer quatre types d’observations :
- Outlier local mais pas global (triangle et cercle rempli)
- Outlier global mais pas local (carré rempli)
- Outlier local et global (losange rempli)
- Ce n’est pas un outlier local ni global
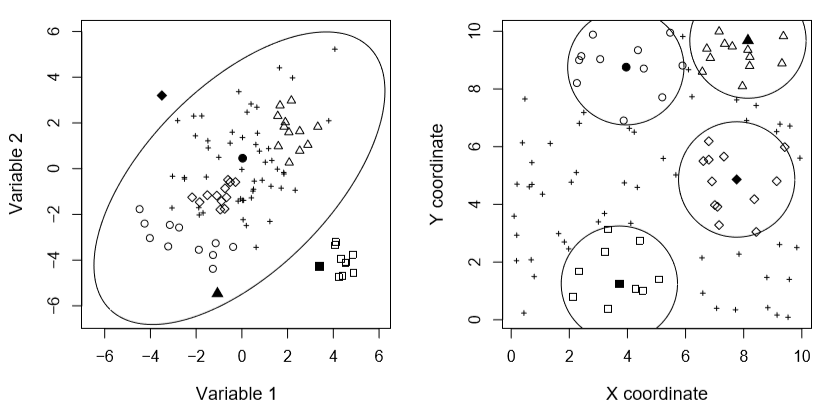
Figure 1. Outliers locaux et globaux (d’après Filzmoser et al., 2014).
Les observations ponctuelles aberrantes, comme on peut l’imaginer, sont des observations qui ont un comportement unique et suspect par rapport à leur voisinage ou à l’ensemble des données (Chandola et al., 2009). Les valeurs aberrantes contextuelles sont des valeurs anormales dans un contexte spécifique mais pas dans un autre (Gao et al., 2010 ; Song et al., 2007). Par exemple, une température de 30° n’est souvent pas une valeur aberrante en été, mais elle peut être considérée comme telle en hiver. Enfin, les valeurs aberrantes régionales constituent un sous-ensemble d’observations étroitement liées – dans l’espace ou non – qui partagent des caractéristiques communes suspectes à l’égard de leur voisinage ou de l’ensemble de données restant (Zhao et al., 2003). La dernière distinction qui peut être faite concerne l’aspect univarié ou multivarié de ces valeurs aberrantes (Chandola et al., 2009). Dans le premier cas, l’ensemble de données ne considère qu’un attribut et une valeur aberrante est définie comme une observation suspecte par rapport à cet attribut (Cousineau et Chartier, 2010 ; Rousseeuw et Hubert, 2011). Dans le cas multivarié, la situation devient plus complexe, car une valeur aberrante peut présenter un comportement normal du point de vue d’un attribut particulier, mais peut avoir un comportement vraiment spécifique selon un autre attribut (Ernst et Haesbroeck, 2013 ; Filzmoser et al., 2014 ; Filzmoser, 2014). La difficulté réside dans la diversité des configurations au sein d’un ensemble de données multivariées.
Les trois approches qui ont été introduites pour définir les concepts clés des valeurs aberrantes sont évidemment liées ! Il est possible d’observer une valeur aberrante locale multivariée ou une valeur aberrante globale ou régionale univariée.
Un petit tour d’horizon des méthodes de détection d’outliers
Étant donné les nombreux domaines d’application qui font appel à la détection d’aberrants, la littérature propose un nombre considérable d’approches qui lui sont consacrées (Kou, 2006 ; Sun, 2006). En général, les techniques de détection des valeurs aberrantes peuvent être classées en 7 grands groupes, chacune basée sur (i) la distribution, (ii) la densité, (iii) la distance (iv) la profondeur, (v) la classification, (vi) le regroupement et (vii) la décomposition spectrale ou la projection des données. Je vous présente rapidement ces grandes familles avec des exemples de méthodes associées entre crochets. Pour les lecteurs motivés et intéressés, une grande partie des références est disponible à la fin du post !
- Distribution-based [modèles gaussiens de mélange, approche bayésienne, estimation du noyau…] : Ces méthodes visent à modéliser la distribution des données avec une fonction connue ou inconnue, c’est-à-dire une approche paramétrique ou non paramétrique (Hawkins, 1980). Les observations dont le comportement est suspect par rapport aux distributions établies sont considérées comme aberrantes (Chhabra et al., 2008 ; Ngan et al., 2016). Des seuils sont souvent fixés pour décider si une valeur diffère significativement de la distribution. Les méthodes paramétriques sont souvent critiquées parce que la distribution des données est le plus souvent inconnue à l’avance.
- Density-based [LOF, LOCI, LoOp…] : Ces approches partent du principe que la densité d’observations à proximité d’une valeur aberrante est sensiblement inférieure à la densité d’observations à proximité d’une valeur attendue ou plus sûre (Breunig et al., 2000 ; Goldstein, 2012 ; Kriegel et al, 2009 ; Papadimitriou et al, 2003 ; Tang et al., 2002). Ces techniques sont parfois préférées aux méthodes basées sur la distance lorsque le jeu de données est composé de sous-ensembles de densités variables. Des seuils sont fixés pour déterminer le voisinage d’une observation et la limite au-delà de laquelle une valeur est considérée comme anormale.
- Distance-based [SLOM, ROF…] : Cette approche utilise la distance entre une observation et l’ensemble des données pour évaluer si cette observation est aberrante ou non (Cai et He, 2010 ; Chawla et Sun, 2005 ; Dang et al, 2015 ; Fan et al, 2006 ; Filzmoser et al, 2014 ; Filzmoser, 2014 ; Harris et al, 2014). Les distances euclidiennes et mahalanobis sont souvent rapportées dans ces méthodes. Plusieurs auteurs ont montré que les estimations courantes de l’emplacement et de l’échelle d’un ensemble de données, c’est-à-dire la moyenne et la variance, sont fortement influencées par les valeurs aberrantes. Des estimations plus robustes ont été élaborées afin que les méthodes fondées sur la distance soient plus fiables (Rousseeuw et Hubert, 2011). Les seuils sont semblables à ceux des méthodes fondées sur la densité.
- Depth-based [KSD…] : L’ensemble de données est modélisé par un ensemble d’enveloppes convexes dont l’objectif est de regrouper les données en fonction de leur proximité au cœur de l’ensemble de données (Chen et al., 2009). Les enveloppes convexes près du noyau de l’ensemble de données contiennent les valeurs les plus attendues tandis que les enveloppes extérieures discriminent les valeurs aberrantes. Le temps de calcul devient excessif lorsque les dimensions de l’ensemble de données dépassent 3 ou 4 (Papadimitriou et al., 2003).
- Classification-based [SVM, approche bayésienne…] : Les méthodes fondées sur la classification peuvent être supervisées ou non (Yang et al., 2010). Dans le premier cas, un jeu de données d’apprentissage pour lequel la position des valeurs aberrantes est connu est utilisé pour construire un classifieur qui permettra de distinguer les valeurs aberrantes dans un ensemble de données de validation. Dans le second cas, le classifieur tente de modéliser l’ensemble des données sans avoir recours à un test ni à un ensemble de données de validation.
- Clustering-based [CLARANS, DBSCAN…] : Ces approches chercher à regrouper les observations en différents sous-ensembles et considèrent que les valeurs aberrantes sont les résidus du processus, c’est-à-dire les observations qui ne sont pas rattachées à un sous-ensemble (Chawla et Gionis, 2013 ; Muller et al., 2012). Intuitivement, les dernières observations à être rattachées sont plus susceptibles d’être aberrantes. Ces méthodes sont parfois critiquées car leur sortie dépend fortement du choix de l’algorithme de clustering. De plus, comme ces approches ont d’abord été essentiellement conçues pour le regroupement (ou clustering) de données, leur potentiel de détection des valeurs aberrantes pourrait être remis en question (Gao et al., 2010 ; Kou, 2006).
- Spectral decomposition-based [PCA, GWPCA…] : Les observations sont projetées sur un nouveau sous-espace pour faciliter la détection des observations aberrantes (Demšar et al. 2013 ; Filzmoser et al, 2007 ; Harris et al., 2014). Cette approche est privilégiée lorsque l’ensemble de données comporte plusieurs dimensions, c.-à-d. lorsque d’autres méthodes ne produiraient pas un résultat dans un délai raisonnable (Fritsch et al., 2011 ; Sun, 2006). Ces techniques apportent une solution au problème dit de la malédiction de la dimensionnalité (« Curse of dimensionality » en anglais, Schubert, 2013 ; Sun, 2006). Ce problème est dû au fait qu’à force d’augmenter le nombre de dimensions des données (le nombre de variables qui les caractérise), les outliers vont être de plus en plus enracinés dans le jeu de données et vont être de plus en plus difficile à détecter. Le nombre de composants principaux à choisir pour la décomposition reste un défi et est toujours défini par un seuil.
Dans la littérature, les méthodes basées sur la distance, la densité et le clustering sont les plus souvent mentionnées. Des approches hybrides, c’est-à-dire combinant plusieurs de ces techniques, ont été proposées par plusieurs auteurs (Harris et al., 2014 ; Mendez et Labrador, 2013).
L’identification des valeurs aberrantes se fait généralement de deux façons, c’est-à-dire par étiquetage ou notation (Kriegel et al., 2009). Les valeurs aberrantes peuvent être étiquetées – étiquetage – ce qui signifie qu’à la fin du processus, on obtient une classification binaire, c’est-à-dire que l’observation est considérée comme aberrante ou non aberrante. D’autres méthodes associent un certain degré d’éloignement aux données (scoring) qui permet d’obtenir un classement des valeurs aberrantes (Muller et al., 2012 ; Papadimitriou et al., 2003). Notez qu’en fixant un seuil aux approches de notation, on obtient une classification binaire comme si les données avaient été étiquetées. Les méthodes de notation sont généralement préférées parce qu’elles permettent d’étudier plus en profondeur l’origine et l’implication des valeurs aberrantes dans les jeux de données.
Dans cette section, on s’est principalement concentrés sur des méthodes de détection, c’est-à-dire que l’on essaye de chercher et trouver les données aberrantes. On pourrait imaginer régler le problème autrement en cherchant à lisser les données et donc par conséquent limiter l’influence de nos petits outliers ! C’est ce qui se passe pas mal dans le domaine du traitement du signal. Je ne rentrerai pas dans le détail de ce type d’approches mais en voici quelques exemples si vous voulez vous documenter :
- Filtres moyens et médians,
- Filtre de Savitsky-Golay,
- Transformée de Fourier,
- Filtres de Wiener et Kalman,
- Soustraction spectrale,
- Transformée en ondelettes,
- Transformée d’Hilbert-Huang [Empirical mode decomposition]
- …
Comment juger de la qualité d’une méthode de détection ?
L’objectif final des méthodes de détection des valeurs aberrantes est d’identifier, aussi bien que possible, et sans confusion, les valeurs aberrantes. Les auteurs s’attachent essentiellement à réduire le nombre de faux positifs (« swamping effect » en anglais), c’est-à-dire à éviter de classer à tort une observation exacte comme une valeur aberrante. Certaines approches considèrent également l’erreur complémentaire à la première (effet de masque) dans laquelle les valeurs aberrantes ne sont pas identifiées comme telles ; ces observations sont classées comme faux négatifs (Ben-gal, 2005 ; Kou, 2006). La caractérisation de ces deux types d’erreurs nécessite évidemment de connaître à l’avance où sont valeurs aberrantes dans l’ensemble de données, ce qui n’est généralement pas le cas. Par conséquent, ces méthodes sont souvent d’abord validées sur des jeux de données synthétiques ou artificiels (dans lesquels des données aberrantes sont volontairement ajoutées) puis appliquées sur des jeux de données réelles. A l’issue du traitement, plusieurs critères peuvent être analysés pour apprécier la pertinence des méthodes proposées. Les études font généralement état de taux de faux positifs et de faux négatifs (Chandola et al., 2009). Les auteurs estiment également la performance de leur classifieur à l’aide de la courbe ROC – un graphique entre les taux de vrais positifs et faux négatifs (Kriegel et al., 2009 ; Zhang et al., 2010). L’amélioration du rapport signal/bruit (SNR) est souvent un critère de bonne qualité dans le cas de signaux uni et multidimensionnels. Plus le rapport est bas, plus la méthode de filtrage est puissante.
Enfin, le temps de calcul des algorithmes doit être sérieusement pris en compte. Avec les systèmes d’acquisition de plus en plus résolus et précis, et avec le stockage d’une grande quantité de données, l’efficacité des classifieurs est une question centrale. Très souvent, les études qui proposent des techniques générales de détection des valeurs aberrantes abordent ce point spécifique (Jin et al., 2006 ; Shekkar et al., 2003 ; Sun, 2006). Les auteurs déterminent l’efficacité de chacune de leurs étapes de traitement afin d’évaluer la scalabilité de leurs méthodes à des jeux de données plus grands et de plus grande dimension.
Que faire une fois qu’on a détecté des outliers ?
Cette question est effectivement une préoccupation majeure après l’identification des valeurs aberrantes. Dans le cas du traitement de signal que j’ai évoqué rapidement (lorsque les signaux unidimensionnels ou multidimensionnels sont lissés), la question n’est plus trop pertinente car l’objectif n’est pas de détecter les valeurs aberrantes mais plutôt de filtrer les jeux de données. Lorsque les valeurs aberrantes sont repérées, deux scénarios sont possibles : les valeurs aberrantes peuvent être supprimées ou corrigées. L’élimination des valeurs aberrantes est brutale mais instantanée. Toutefois, la taille du jeu de données peut être considérablement réduite si on se trouve en présence d’une grande quantité de valeurs aberrantes. C’est également critiquable si les méthodes de détection aberrantes ne sont pas robustes. Par exemple, si le taux de faux positifs est important, c’est-à-dire qu’un objet est identifié à tort comme étant une valeur aberrante, la suppression des valeurs aberrantes entraînera la suppression d’observations pertinentes. La correction d’une valeur aberrante est un problème plus complexe. Il est effectivement possible d’utiliser le voisinage d’une observation ou certains patrons/motifs généraux dans les données pour modifier la valeur d’une observation aberrante, mais ces méthodes sont susceptibles d’ajouter du bruit dans les jeux de données si on ne fait pas ce travail avec beaucoup de précaution. Une possibilité de correction serait de remplacer une valeur aberrante par le résultat d’une interpolation à partir d’objets voisins. Mais on prend à ce moment-là le risque de lisser les informations de notre jeu de données, il faut en être conscient…
Inconvénients et limites des méthodes actuelles : application générale et automatisation
La plupart des méthodes de détection décrites précédemment utilisent des seuils manuels pour le filtrage des données. Toutefois, est-il vraiment concevable d’appliquer des seuils similaires à deux ensembles de données qui ont été acquis dans des conditions particulièrement différentes ? Comment est-il possible de traiter rapidement un grand nombre d’ensembles de données s’il est nécessaire de déterminer manuellement de nouveaux seuils à chaque nouvel ensemble de données ?
Toutes les méthodes de détection d’aberrants qui ont été présentées ont besoin de seuils à différents niveaux pour identifier les valeurs aberrantes. Le choix de ces seuils peut avoir un impact considérable sur la détection des valeurs anormales. Par exemple, un des premiers seuils à fixer a rapport avec l’établissement d’un voisinage pour chaque observation (Breunig et al., 2000 ; Knorr et al., 1998). Ce seuil correspond souvent à une distance au kième voisin ou à une distance qui assure que k voisins appartiennent au voisinage d’une observation. Dans les approches de notation (scoring), le seuil au-delà duquel une observation est considérée comme aberrante est crucial. Un seuil bas augmenterait le taux de faux négatifs alors qu’un seuil élevé augmenterait le taux de faux positifs. D’un point de vue général, l’interprétation des notes est une tâche relativement complexe pour les non spécialistes. Ces scores sont souvent très différents d’une méthode à l’autre et peuvent avoir des significations complètement différentes. Certains auteurs ont tenté de simplifier ces scores en les échelonnant entre 0 et 1 afin qu’ils puissent être compris dans une approche probabiliste, plus simple à manipuler ; une valeur de 1 indiquant qu’un objet a 100% de chance d’être considéré comme un aberrant (Kriegel et al., 2009). Même si la méthode est plus pratique, fixer un seuil entre 0 et 1 reste difficile et soumis à expertise.
On peut également rajouter que la plupart des méthodes de filtrage signalées doivent être appliquées dans des conditions spécifiques. Plusieurs approches de traitement du signal exigent que les signaux d’entrée soient linéaires ou stationnaires. Certaines méthodes de détection des valeurs aberrantes sont limitées a priori par les distributions ou le type de données d’entrée. Afin de développer des outils très généraux et automatisés, ces pré-requis constituent un véritable obstacle. C’est un obstacle qui empêche certaines méthodes d’être utilisées sur des données multiples et diverses. Évidemment, les méthodes générales sont moins puissantes que les méthodes spécifiques, mais elles peuvent être utilisées de façon un peu plus étendue.
Références
Ben-gal, I. (2005). Outlier detection, 1–16.
Breunig, M. M., Kriegel, H.-P., Ng, R. T., & Sander, J. (2000). LOF: Identifying Density-Based Local Outliers. Proceedings of the 2000 Acm Sigmod International Conference on Management of Data, 1–12. http://doi.org/10.1145/335191.335388
Cai, Q., & He, H. (2010). IterativeSOMSO : An iterative self-organizing map for spatial outlier detection. Theoretical Computer Science, (March). http://doi.org/10.1007/978-3-642-13318-3
Cai, Q., He, H., & Man, H. (2013). Spatial outlier detection based on iterative self-organizing learning model. Neurocomputing, 117, 161–172. http://doi.org/10.1016/j.neucom.2013.02.007
Chandola, V., Banerjee, A., & Kumar, V. (2009). Outlier Detection : A Survey.
Chawla, S., & Gionis, A. (2013). k -means– : A unified approach to clustering and outlier detection.
Chawla, S., & Sun, P. (2005). SLOM: A new measure for local spatial outliers. Knowledge and Information Systems, 9(4), 412–429. http://doi.org/10.1007/s10115-005-0200-2
Chen, Y., Dang, X., Peng, H., & Bart, H. L. (2009). Outlier detection with the kernelized spatial depth function. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(2), 288–305. http://doi.org/10.1109/TPAMI.2008.72
Chhabra, P., Scott, C., Kolaczyk, E. D., & Crovella, M. (2008). Distributed spatial anomaly detection. Proceedings – IEEE INFOCOM, 2378–2386. http://doi.org/10.1109/INFOCOM.2007.232
Cousineau, D., & Chartier, S. (2010). Outliers detection and treatment : a review . Internation Journal of Psychological Research, 3(1), 58–67.
Dang, T., Ngan, H. Y. T., & Liu, W. (2015). Distance-Based k -Nearest Neighbors Outlier Detection Method in Large-Scale Traffic Data, (February 2016). http://doi.org/10.1109/ICDSP.2015.7251924
Ernst, M. and Haesbroeck, G. (2013). Robust detection techniques for multivariate spatial data. Poster.
Fan, H., Zaïane, O. R., Foss, A., & Wu, J. (2006). A nonparametric outlier detection for effectively discovering top-N outliers from engineering data. Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 3918 LNAI, 557–566. http://doi.org/10.1007/11731139_66
Filzmoser, P. (2004). A multivariate outlier detection method. Seventh International Conference on Computer Data Analysis and Modeling, 1(1989), 18–22. Retrieved from http://computerwranglers.com/com531/handouts/mahalanobis.pdf
Filzmoser, P., Maronna, R., & Werner, M. (2007). Outlier identification in high dimensions. Filzmoser, P. Maronna, R. Werner, M. http://doi.org/10.1016/j.csda.2007.05.018
Filzmoser, P., Ruiz-gazen, A., & Thomas-agnan, C. (2014). Identification of local multivariate outliers.
Fritsch, V., Varoquaux, G., Thyreau, B., Poline, J.-B., & Thirion, B. (2011). Detecting Outlying Subjects in High-Dimensional Neuroimaging Datasets with Regularized Minimum Covariance Determinant. Medical Image Computing and Computer-Assisted Intervention, Miccai 2011, Pt Iii, 6893, 264–271. Retrieved from <Go to ISI>://WOS:000306990200033
Gao, J., Liang, F., Fan, W., Wang, C., Sun, Y., & Han, J. (2010). On community outliers and their efficient detection in information networks. Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’10), 813–822. http://doi.org/10.1145/1835804.1835907
Goldstein, M. (2012). FastLOF: An Expectation-Maximization based Local Outlier detection algorithm, (1), 2282–2285.
Griffin, T., Dobbins, C., Vyn, T., Florax, R., & Lowenberg-DeBoer, J. (2008). Spatial analysis of yield monitor data: case studies of on-farm trials and farm management decision making. Precision Agriculture, 9(5), 269–283. http://doi.org/10.1007/s11119-008-9072-2
Harris, P., Brunsdon, C., Charlton, M., Juggins, S., & Clarke, A. (2014). Multivariate Spatial Outlier Detection Using Robust Geographically Weighted Methods. Math Geosciences, 1–31. http://doi.org/10.1007/s11004-013-9491-0
Jin, W., Tung, A. K. H., Han, J., & Wang, W. (2006). Ranking outliers using symmetric neighborhood relationship. Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 3918 LNAI, 577–593. http://doi.org/10.1007/11731139_68
Knorr, E. M., & Ng, R. T. (1998). Algorithms for Mining Datasets Outliers in Large Datasets. Proceedings of the 24th VLDB Conference, New York, USA.
Kou, Y. (2006). Abnormal Pattern Recognition in Spatial Data.
Kou, Y., Lu, C., & Chen, D. (2006). Spatial Weighted Outlier Detection. In Proceedings of SIAM Conference on Data Mining, 613–617. http://doi.org/10.1137/1.9781611972764.71
Kriegel, H., Kröger, P., Schubert, E., & Zimek, A. (2009). LoOP : Local Outlier Probabilities. Proceeding of the 18th ACM Conference on Information and Knowledge Management – CIKM ’09, 1649. http://doi.org/10.1145/1645953.1646195
Lu, C.-T., Chen, D., & Kou, Y. (2003). Algorithms for spatial outlier detection. Third IEEE International Conference on Data Mining, 0–3. http://doi.org/10.1109/ICDM.2003.1250986
Mendez, D., & Labrador, M. A. (2013). On Sensor Data Verification for Participatory Sensing Systems. Journal of Networks, 8(3), 576–587. http://doi.org/10.4304/jnw.8.3.576-587
Muller, E., Assent, I., Iglesias, P., Mulle, Y., & Bohm, K. (2012). Outlier Ranking via Subspace Analysis in Multiple Views of the Data.
Ngan, H. Y. T., Lam, P., & Yung, N. H. C. (2016). Outlier Detection In Large-scale Traffic Data By Naïve Bayes Method and Gaussian Mixture Model Method, (February).
Papadimitriou, S., Kitagawa, H., Gibbons, P. B., & Faloutsos, C. (2003). LOCI: fast outlier detection using the local correlation integral. Proceedings 19th International Conference on Data Engineering (Cat. No.03CH37405), 315–326. http://doi.org/10.1109/ICDE.2003.1260802
Rousseeuw, P. J., & Hubert, M. (2011). Robust statistics for outlier detection. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 1(1), 73–79. http://doi.org/10.1002/widm.2
Schubert, E. (2013). Generalized and efficient outlier detection for spatial, temporal, and high-dimensional data mining. Retrieved from http://nbn-resolving.de/urn:nbn:de:bvb:19-166938
Song, X., Wu, M., Jermaine, C., & Ranka, S. (2007). Conditional Anomaly Detection. IEEE Transactions on Knowledge and Data Engineering, (0325459), 1–14.
Sun, P. (2006). Outlier Detection in High Dimensional , Spatial and Sequential Data Sets.
Taylor, J. A., Mcbratney, A. B., & Whelan, B. M. (2007). Establishing Management Classes for Broadacre Agricultural Production. Agronomy Journal, 1366–1376. http://doi.org/10.2134/agronj2007.0070
Zhang, Y., Meratnia, N., & Havinga, P. (2010). Outlier Detection Techniques for Wireless Sensor Networks: A Survey. IEEE Communications Surveys & Tutorials, 12(2), 1–12. http://doi.org/10.1109/SURV.2010.021510.00088
Zhao, J., Lu, C., & Kou, Y. (2003). Detecting Region Outliers in Meteorological Data, 49–55.
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

