Construire un variogramme théorique
L’intérêt des variogramme dans les études d’Agriculture de Précision a largement été mise en avant dans un post précédent. C’est effectivement un outil très utile pour étudier la variabilité spatiale des données spatiales agronomiques et environnementales. Ce post met en avant un jeu de données qui a été créé en suivant la méthodologie du post suivant : « Simulation de données spatiales avec une structure spatiale connue ». Ce jeu de données est un dataframe (un tableau) avec trois colonnes : la longitude (x), la latitude (y) et la variable d’intérêt (le rendement, RDT).
## Chargement des packages d'intérêt
library(gstat)
library(sp)
head(RDT_gaussian_field)
x y RDT
1 1 1 7.788309
2 2 1 7.692076
3 3 1 8.433189
4 4 1 8.147506
5 5 1 9.124606
6 6 1 8.733661
class(RDT_gaussian_field)
[1] "data.frame"
## Transformation du dataframe en SpatialPointDataFrame
## L'objectif est d'aboutir à un objet spatial
coordinates(RDT_gaussian_field)=~x+y
class(RDT_gaussian_field)
[1] "SpatialPointsDataFrame"
attr(,"package")
[1] "sp"
## Si les coordonnées ne sont pas projetées (ex : si elles sont exprimées en degrés), il faut d'abord reprojeter les observations.
## Ici, ce n'est pas nécessaire parce que les observations sont positionnées sur un grille régulière
## Calcul du variogramme
Vario_RDT=variogram(RDT~1, ## Ici, on assume qu'il y a une tendance constante dans les données. Par exemple, ça n'aurait pas
## été le cas pour une étude de l'altitude le long d'une pente parce qu'il y aurait eu un gradient
## d'altitude clair en relation avec les coordonnées spatiales des observations (le long de la pente)
data=RDT_gaussian_field)
## Afficher le variogramme expérimental
plot(Vario_RDT)
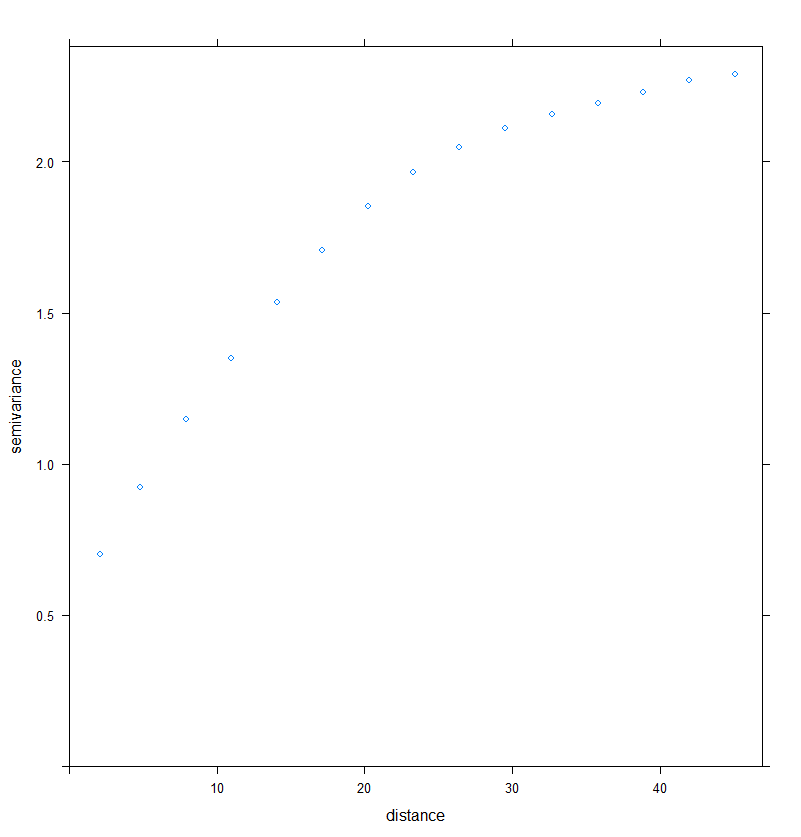
Figure 1. Construction du variogramme expérimental
Ajuster un modèle de variogramme aux données
Une fois que le semi-variogramme a été créé, l’objectif est d’ajuster un modèle de smi-variogramme aux données pour décrire au mieux la structure spatiale du jeu de données d’intérêt. Cela peut être fait comme suit :
## Ajustement d'un modèle de variogramme aux données
Vario_RDT.fit = fit.variogram(Vario_RDT,
## Un modèle de semi-variogramme doit être proposé manuellement pour commencer mais c'est
## seulement pour orienter l'ajustement! Les paramètres vont certainement un peu changer après l'ajustement
model = vgm(psill=2, ## Partial Sill = Pallier Partiel (à ne pas confondre avec le pallier)
model="Sph", ## Un modèle sphérique semble approprié
range=30, ## Portée pratique = distance maximale d'auto-corrélation
nugget=0.5)) ## Effet pépite = Variations à petite échelle (courtes distances)
## Regarder les résultats de l'ajustement
> Vario_RDT.fit
model psill range
1 Nug 0.5610564 0.00000
2 Sph 1.6354986 33.53541
## La première estimation des paramètres était relativement bonne donc les sorties sont très proches des paramètres
## rentrés manuellement.
## Afficher le variogramme avec le modèle correspondant
plot(Vario_RDT,Vario_RDT.fit)
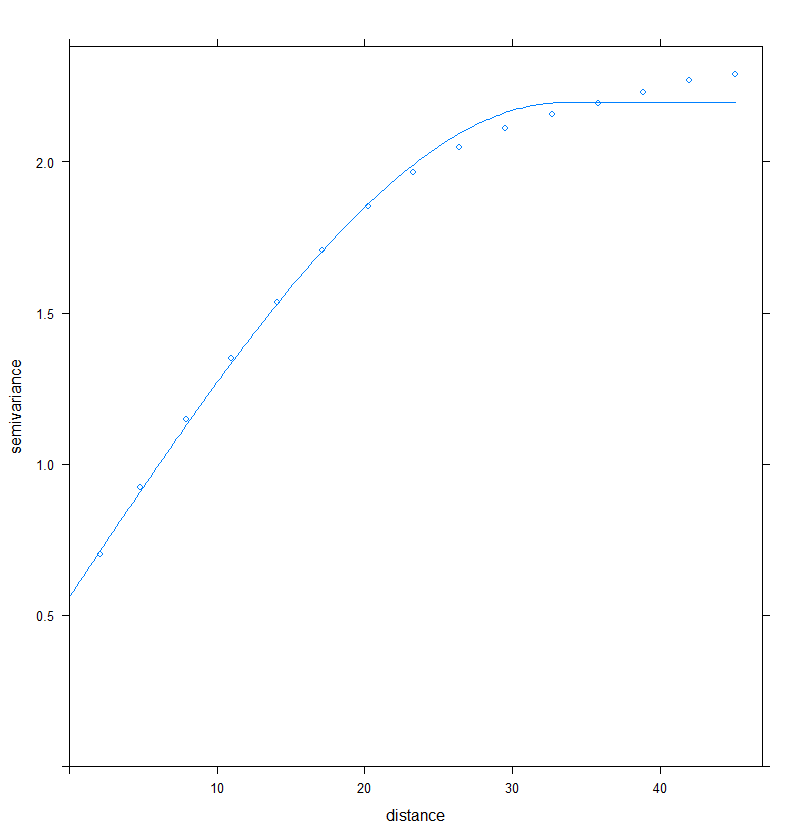
Figure 2. Ajustement d’un modèle au variogramme expérimental
Vers une caractérisation plus fine du variogramme
Les précédentes sections de code avaient pour objectif d’afficher un variogramme expérimental et d’y ajuster un modèle de semi-variogramme. Tous les paramètres de la fonction variogram du package ‘gstat’ ont été utilisés par défaut. Néanmoins, dans certains cas, il est important de jouer avec ces paramètres pour être sûrs que le variogramme est affiché correctement. Parmi ces réglages, deux paramètres sont à prendre en compte : cutoff and width. Le ‘cutoff’ représente la distance spatiale maximale qui est prise en compte entre deux observations. Le paramètre ‘width’ contrôle l’intervalle de distance sur lequel la semi-variance est calculée
## Choix des paramètres cutoff et width dans la fonction du variogramme
Vario_RDT=variogram(RDT~1,data=RDT_gaussian_field,cutoff=30,width=5)
Vario_RDT=variogram(RDT~1,data=RDT_gaussian_field,cutoff=60,width=5)
Vario_RDT=variogram(RDT~1,data=RDT_gaussian_field,cutoff=90,width=10)
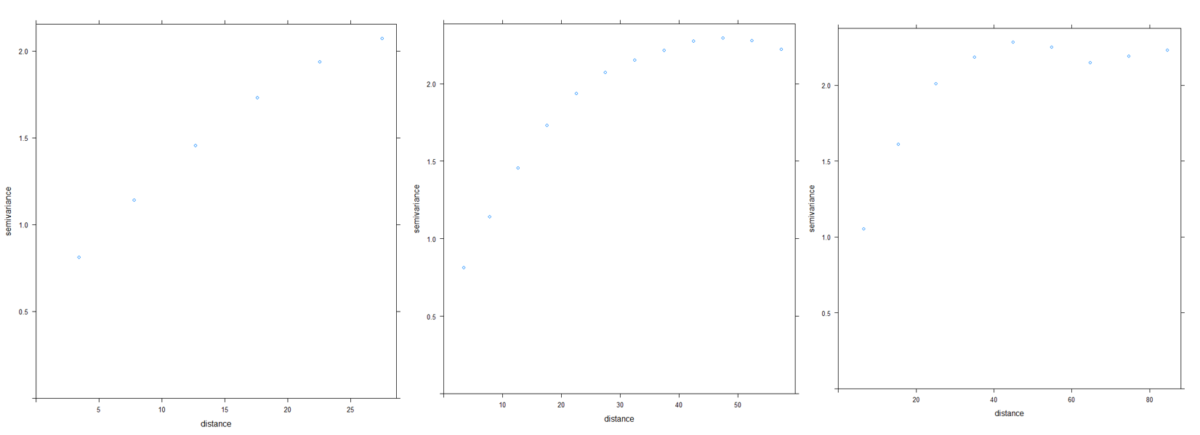
Figure 3. Variogrammes expérimentaux et paramétrage du « cutoff » et « width »
A noter que si le cutoff est trop faible, certaines structures spatiales pourraient être manquées ou la structure spatiale globale pourrait être mal comprise. Si le paramètre width est réglé trop haut, la structure spatiale sera lissée et de l’information utile est susceptible d’être perdue. Réaliser une analyse variographique demande de régler avec précaution les paramètres du variogramme pour que la structure spatiale soit bien déterminée.
Phénomène isotropique ou anisotropique ? Création de variogrammes directionnels
Jusqu’à présent, les phénomènes qui ont donné naissance aux données ont été considérés comme isotropiques, c’est à dire qu’ils n’évoluent pas différemment en fonction d’une direction d’intérêt dans l’espace. Néanmoins, quelquefois, un facteur extérieur (pente, température) peut affecter la structure spatiale d’un jeu de données. Il est alors nécessaire de créer des variogrammes directionnels. Ces variogrammes sont créés de la même façon que précédemment sauf que de nouveaux paramètres doivent être réglés.
## Choix des directions d'intérêt dans lesquelles calculer les variogrammes
RDT_vario.dir=variogram(RDT~1,
data=RDT_gaussian_field,
alpha = c(0, 45, 90, 135))
## Les semi-variogrammes seront affichés dans les directions 0, 45, 90 et 135°
## Le variogramme est une mesure symmétrique donc par exemple, les directions 45 et 225° (45+180)
## vont conduire aux même résultats
## Afficher les variogrammes directionnels
plot(RDT_vario.dir)
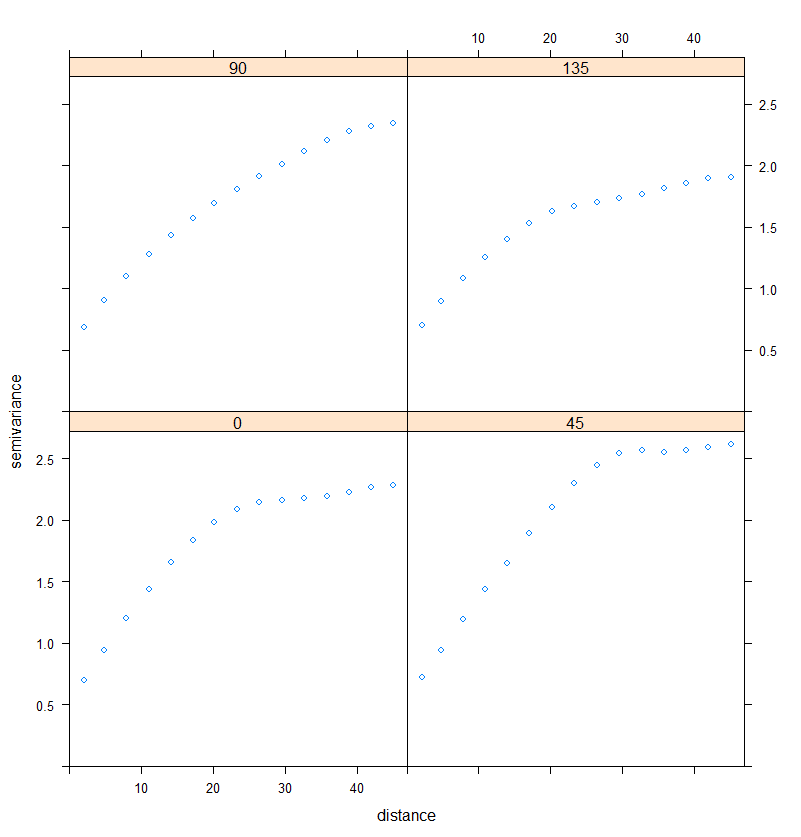
Figure 4. Variogrammes directionnels
Il faut noter que ces variogrammes sont créés dans les directions demandées avec un certain degré de tolérance par rapport à ces directions
Par exemple, si la direction 45° est choisie, comment gérer les paires d’observations dont la direction entre ces observation est 59° ? Faut-il les supprimer ?
Par défaut, le calcul est rapporté à la direction demandée la plus proche.
Par exemple, dans la précédente section de code avec les directions 0, 45, 90 et 135°, l’intervalle entre les directions est de 45°. Chaque variogramme directionnel est la synthèse des variogrammes sur les directions X +/- 22.5° (45 divisé par 2). Par exemple, le variogramme directionnel dans la direction 90° prend en compte toutes les directions entre 67.5 et 112.5°
La tolérance peut être réglée avec les paramètres tol.hor (tolérance horizontale) et tol.ver (tolérance verticale) dans la fonction variogram du package gstat. Finalement, il y a également la possibilité d’ajuster un modèle de variogramme aux variogrammes directionnels précédemment établis. A noter qu’un modèle ne peut pas être ajusté à tous les variogrammes directionnels en même temps. Seul un modèle est fourni.
## Ajuster un modèles de semi-variogramme aux variogrammes directionnels.
RDT_variodir.fit = vgm(psill=2, ## Un modèle de semi-variogramme est estimé à l'oeil comme précédemment
model="Sph",
range=30,
nugget=0.5,
## Choix des paramètres d'anisotropie. Ils doivent aussi être estimés à l'oeil
anis = c(45, ## Direction de la portée la plus forte par rapport à toutes les directions affichées.
## Ici, la direction 45° semble être celle avec la plus grande portée
0.6)) ## Ratio de la plus petite portée (autour de 25m)
## sur la plus grande portée (autour de 40m)
## Afficher les variogrammes directionnels et les modèles correspondants
plot(RDT_vario.dir, RDT_variodir.fit)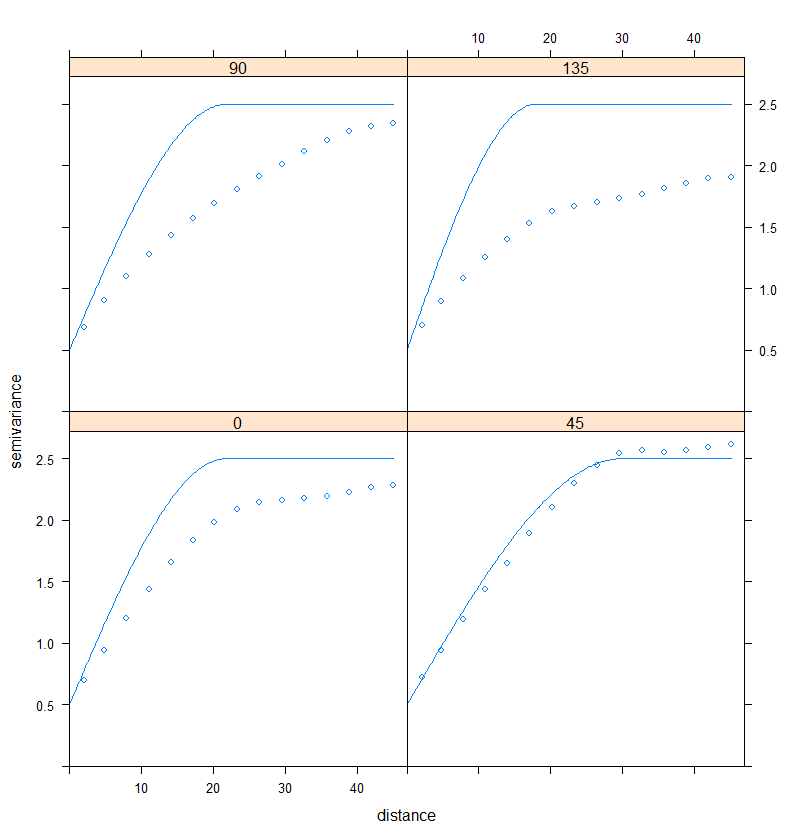
Figure 5. Ajustement d’un modèle de variogramme aux variogrammes directionnels
En regardant la figure 5, il semble que la structure spatiale soit relativement plus forte dans les directions 0 et 45°. Pour réaliser une analyse plus précise, il faudrait tester d’autres directions et régler les paramètres de tolérance angulaire. Les variogrammes directionnels sont un outil très utile pour mettre en avant une direction prépondérante de variabilité. Dans le cas présent, le phénomène peut être considéré comme isotropique parce que les différences ne sont pas extrêmement fortes entre les directions étudiées.
Avec tout ce qui a été dit, il faut bien comprendre qu’il faut garder une supervision manuelle lorsque l’on réalise des analyses variographiques. Je ne recommanderais pas d’automatiser les étapes qui ont été présentées au risque d’arriver à des conclusions erronées. Si la structure spatiale est très claire et vraiment bien définie, cela ne devrait pas poser problème. Néanmoins, dans la plupart des cas, un ajustement automatique d’un modèle de semi-variogramme peut poser des problèmes.
Soutenez les articles de blog d’Aspexit sur TIPEEE
Un p’tit don pour continuer à proposer du contenu de qualité et à toujours partager et vulgariser les connaissances =) ?

